Day 11 - BST 二叉树4
之前我们已经学习了二叉树的结构和常用的面试技巧——递归、BFS、DFS。这节课我们来看看2018年谷歌面试中出现过的一道二叉树面试题。
1.案例: 统计完全二叉树的节点数
给定一棵完全二叉树,计算它的节点数。
输入:
输出: 6
思路分析
完全二叉树是一种常考的数据结构,在一般二叉树的基础上要求每一层从左到右都需要填满,不能有空缺,最后一行可以在右侧有空缺。下图就是一棵完全二叉树
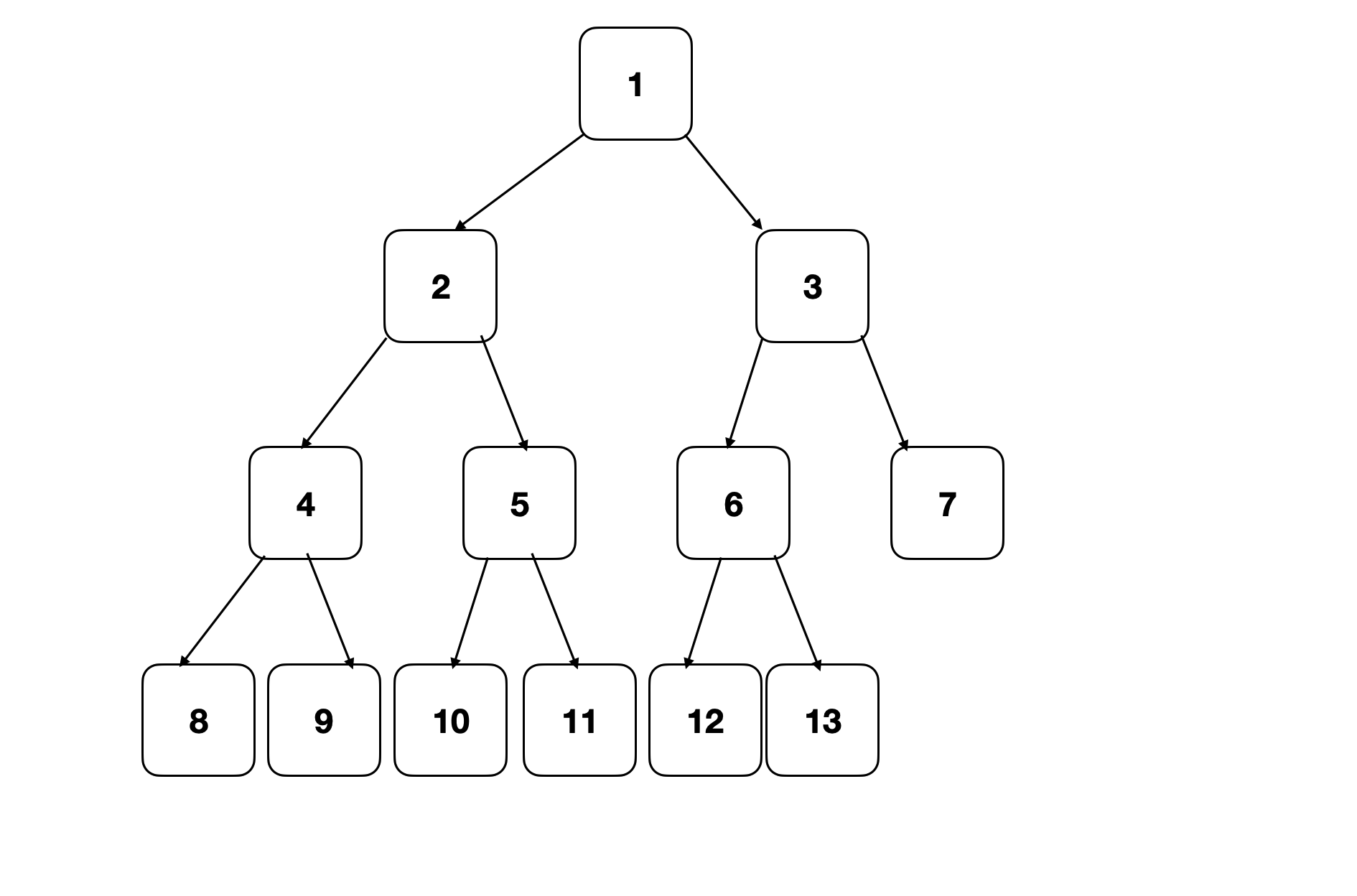
对于二叉树的面试题,通用的思路包含了三个步骤。
- 是否需要遍历整棵树
- 是否利用二叉树的性质(树是否平衡、左右子树是否有大小上的相关性、父节点与子节点有没有额外的关系)
- 这些可以利用的性质中,有哪些可以帮我们得到更快的算法
对于本题,我们首先要做的是分析:哪些条件以及明确给出,哪些条件过于模糊需要与面试官讨论。比如:
- 树与节点的具体定义是什么样的
- 树的大小有多大范围
- 整棵树是否可以被载入内存
- 节点上的数字是已经给出,还是需要自己计算
- ……
询问面试官后,我们至少可以得到以下信息:
- 整棵树可以在内存中处理
- 每个节点上的数字可以用
Integer number表示 - 该数字是一个虚拟的标签,并不是节点的一部分
- ……
再结合上面提到的二叉树三步思路,我们可以首先抛出一个暴力解来与面试官沟通
解法1
将整棵树遍历一遍,经过所有节点,挨个统计,最后返回所有节点的个数。
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
return countNodes(root.right) + countNodes(root.left) + 1;
}
}
这种方法最简单粗暴,易于实现,时间消耗O(N)。从面试官的角度,如果这道题只做到这一步,只能收获lean no hire的评价。
谷歌的评价标准分为六个等级,按照面试者的水平: strongly no hire < no hire < lean no hire < lean hire < hire < strongly hire 一般而言,只有在多轮面试中都拿到hire的面试者,才有机会被送到hiring committee, 由更高一级的委员会来评价
上面这种解法既没有利用好二叉树的性质,也没有将标签上的数字利用上
解法2
第二种解法,利用了完全二叉树的定义,即每一层一定是从左到右填满的。
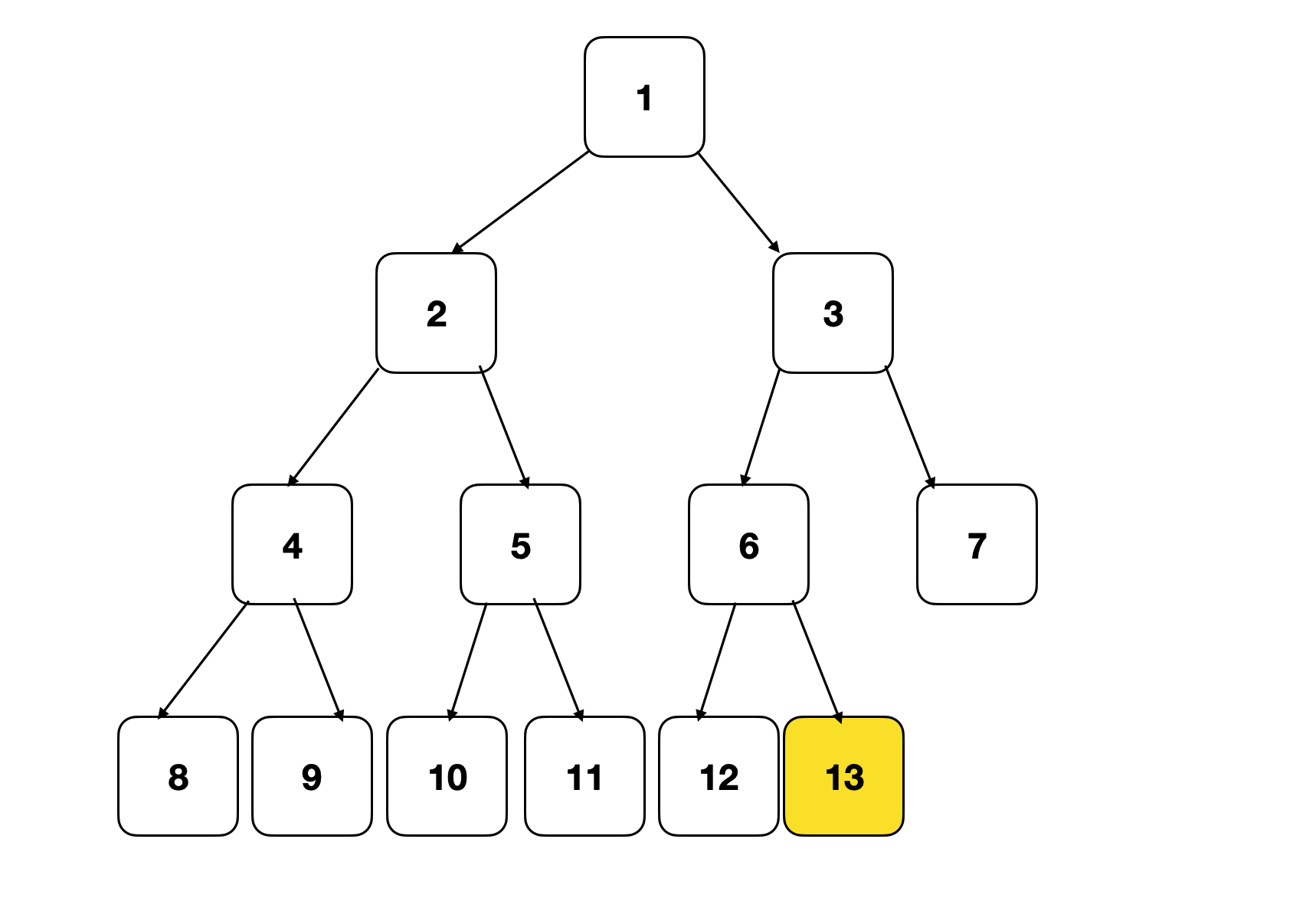
比如图中,第四层只有左侧是填满的,最后一个数字13正是树的节点数。这样我们就将判断树的节点个数,等价成了寻找最大编号节点的问题。
我们可以用尝试用自然语言描述这样一个算法:首先,将从节点到树根的距离定义为深度。接下来利用二分法找到最后一个深度为4的节点,即为最大编号节点。
- 从树根开始,先沿着左分支一直到叶子节点(8),得到最大深度4。
- 从根节点的右节点3开始,沿着左分支到达12,同样最大深度为4。这说明最大编号节点大于等于12
- 从3的右节点7开始继续沿左分支到达叶子节点(7),最大深度为3,说明最大编号小于(14) ……
使用二分法在每个分支依次寻找叶子节点,并比较最大深度,经过 logN 次寻找, 得到最大编号即为树的结点数。每次寻找需要经过 logN 个节点,时间复杂度为log2N。
这种方法利用了二叉树的性质,优化了查找速度。如果能够在规定时间内实现,面试官应该给出hire的评价。缺点是这种方法实现复杂,容易出bug。对于立志于进入大厂的同学,不应满足于一个能用的解法,我们需要更进一步追求strongly hire的评级。
解法3
第三种方法在解法2基础上进行了优化,同样利用了二分法。解法3和解法2在实现上是等价的,只不过由于解题的方向不同,解法3比解法2更容易实现。
首先,解法3需要一个辅助函数来判断某个编号是否存在于树中
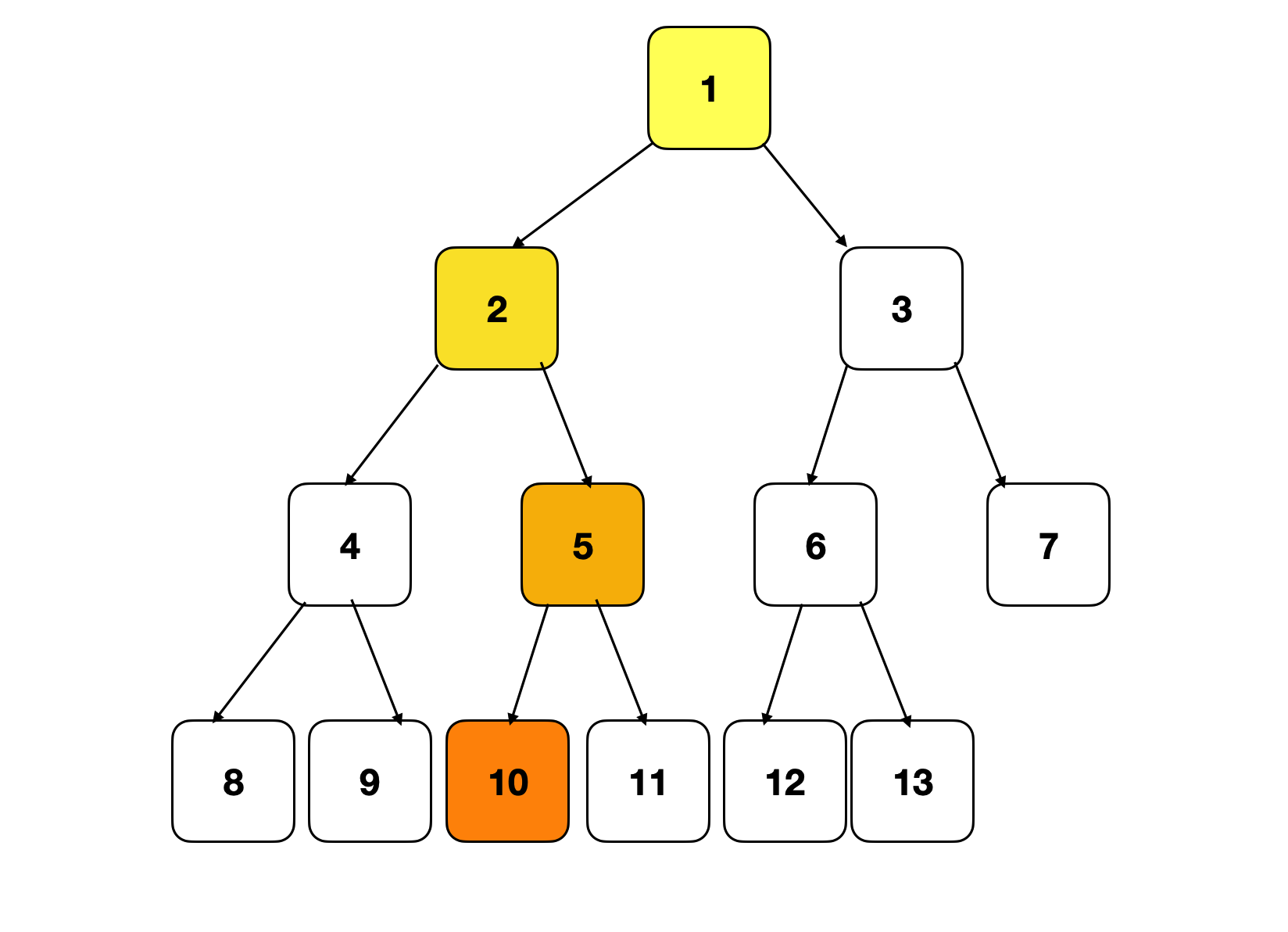
比如我们想知道图中的树是否包含节点10。
根据这棵树的性质,父节点的编号等于子节点编号除以2。如果存在节点10,那么它与根节点的路径应该是10 - 5 - 2 - 1
List<Integer> findPath(int num) {
ArrayList<Integer> path = new ArrayList<>();
while (num != 0) {
path.add(num);
num /= 2; // 每次用子节点编号除以2,获得父节点编号
}
Collections.reverse(path);
return path;
}
我们可以从根节点出发,按照1 -> 2 -> 5 -> 10的顺序去判断每个节点是否存在,如果全部存在,那么这棵树包含节点10。反之,节点10并不存在。
public boolean exist(TreeNode root, int num) {
List<Integer> path = findPath(num);
for (int i = 1; i < path.size(); i++) {
if (root == null)
return false;
// 根据子节点编号和父节点编号的关系,判断分支的左右关系
root = path.get(i) % 2 == 0 ? root.left : root.right;
}
return root != null;
}
PS. 这个辅助函数是可以优化的. 1 -> 2 -> 5 -> 10的路径上,对分支选择仅仅依赖于数字的奇偶性,而非具体数值,三次选择依次为左右左。
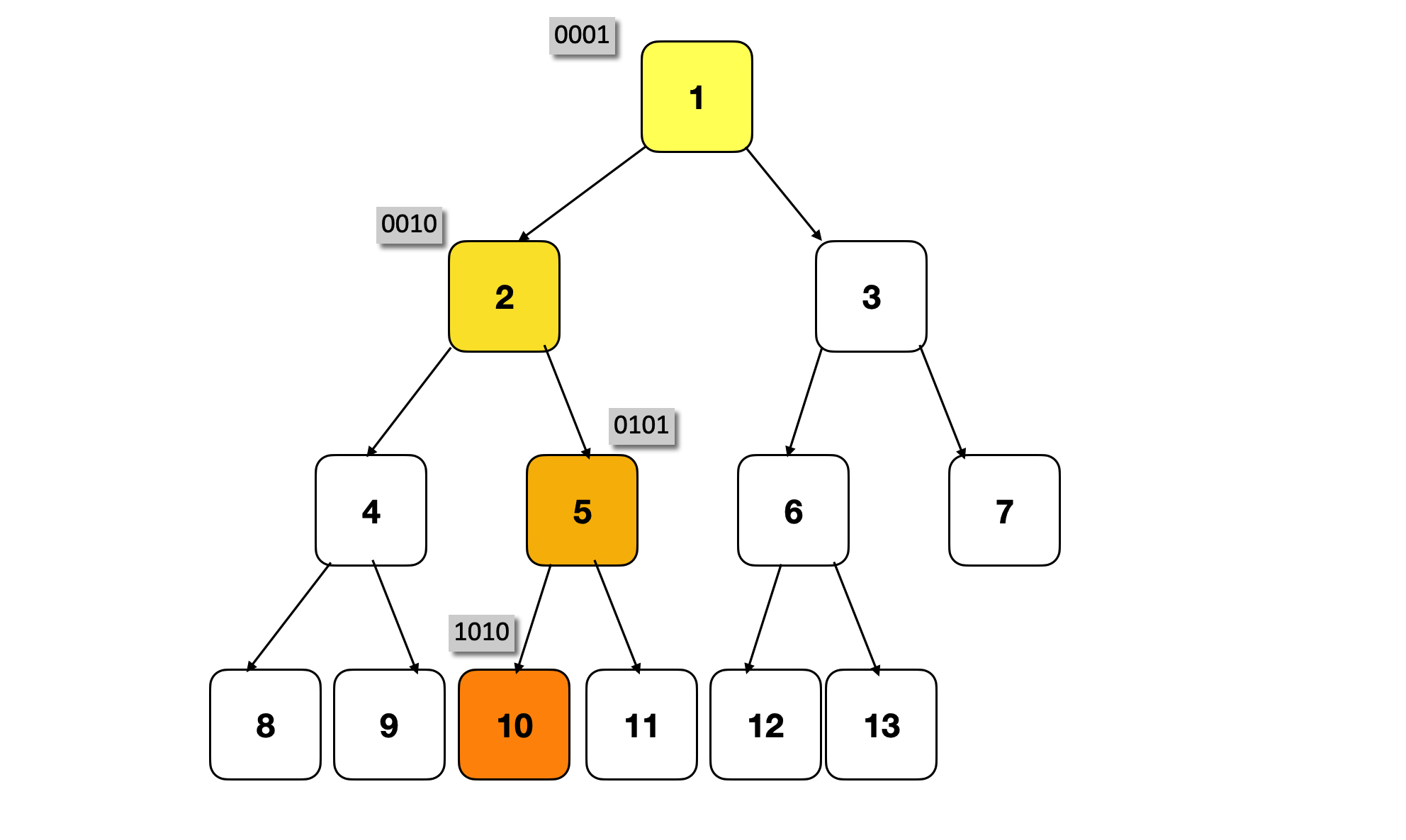
我们可以利用目标节点10的二进制表达1010,来省略预计算路径的步骤,甚至将这一步的计算近似看成O(1)操作。
算法上,我们将第1个bit略过,第2个bit开始0代表左、1代表右。比如节点10(1010),去掉第1个bit得到010, 对应左右左
boolean exist(TreeNode root, int num) {
for (int pivot = Integer.highestOneBit(num) / 2; pivot != 0; pivot /= 2) {
if (root == null)
return false;
root = (num & pivot) == 0 ? root.left : root.right;
}
return root != null;
}
有了辅助函数exist之后,接下来我们的问题就可以等加成,在一个给定的连续范围1 ~ N中,判断N的具体值。因为1 ~ N是一个连续的范围,所以我们可以利用二分法来查找(我们会在之后的章节里详细介绍二分法的模板写法):
public int countNodes(TreeNode root) {
int max = 1;
while (exist(root, max)) {
max *= 2; // 找到N的上限
}
int min = 1;
while (min + 1 < max) { // 利用二分法模板,在min ~ max之间寻找N
int mid = min + (max - min) / 2;
if (exist(root, mid)) {
min = mid;
} else {
max = mid;
}
}
return exist(root, max) ? max : min;
}
总结
本章我们通过一道经典面试题,实践了二叉树考题的三步解题思路。对于这类经验性的题目,最好的方法就是不断练习。建议使用Leetcode 270, 958 作为课后习题
习题
- 给定一棵二叉树,判断它是不是一颗完全二叉树