Day 17 - Graph 图 1
在之前的章节中,其实我们已经见识过一些图的问题了。链表、树、甚至数组都是图论问题的一小部分。树是图的子集,而链表又是树的子集。这节课开始我们将从特例推广到一般,来学习图论的知识。
基础知识——图与树
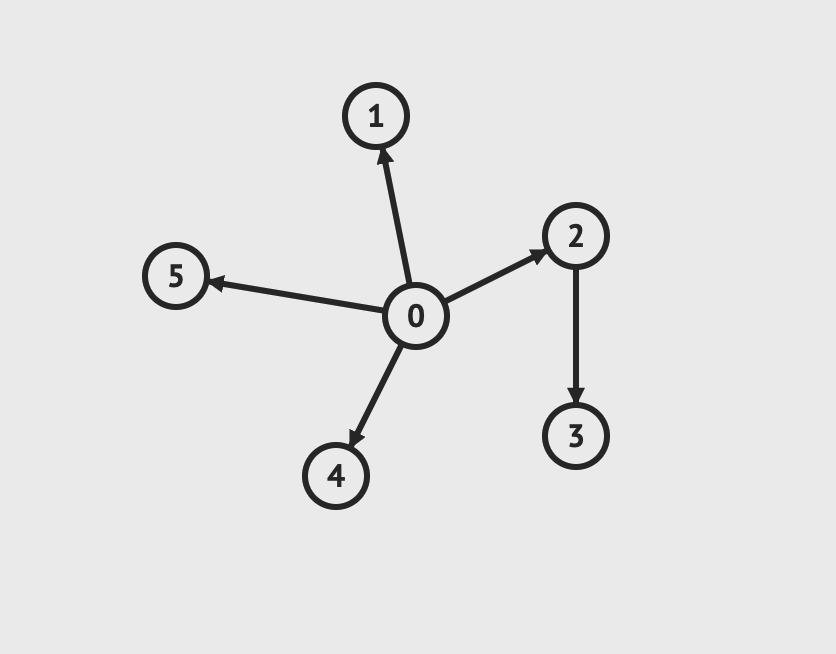
在之前的章节里我们已经学习了树,尤其是二叉树。在图论中,树是一种连通图,其中任意两个顶点间存在唯一一条路径。下面这张图,其实也是一棵树。
图片由visualgo制作
如果在树的基础上加上环路,那么就会变成图。
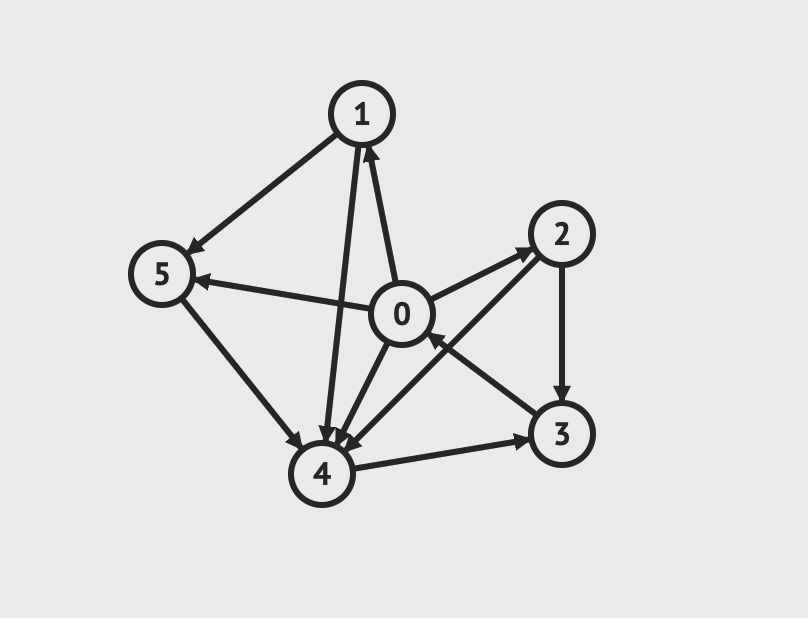
图片由visualgo制作
从面试题的角度来看,树类问题是链表问题的进阶,图类问题是树类问题的进阶。
基础知识——树搜索
我们之前学习了BFS和DFS两种搜索算法。树类搜索有一种通用模板,我们用伪代码来描述。
首先我们先约定每个节点的结构:每个节点包含当前节点的值value,一个children列表包含所有当前节点的子节点(子节点可能有0个或多个)
class Node {
int value;
List<Node> children;
}
假设我们要在一棵树上寻找一个target节点。我们定义tree_search函数,函数接收根节点root、目标节点target、数据队列sequence。
这里要注意数据队列sequence并不是指Queue结构,sequence代表了数据接收和处理的顺序。
- 当sequence时LIFO队列时,表现为Stack。
- 当sequence时FIFO队列时,表现为Queue。
数据队列sequence通过add向结构中添加一个元素,通过remove从结构中取出一个元素。
// 接收根节点root、目标节点target、数据队列sequence
function tree_search(sequence, root, target):
sequence = {root} // 初始化sequence,并向其中添加root节点
while sequence is not empty: // 当sequence中还有元素存在是
curt = sequence.remove() // 从sequence中取出一个元素
if curt == target: // 如果遇上target,说明找到目标
return true
for (Node child : curt.children) // 扩展搜索的范围
sequence.add(child) // 将当前节点所有的子节点添加进sequence
return false // 当sequence为空时还没有找到target
// 如果将Queue传入tree_search
// sequence将按照FIFO先进先出的顺序添加和弹出元素,会得到BFS算法
function breadth_first_search(root, target):
return tree_search(new Queue(), root, target)
// 如果将Stack传入tree_search
// sequence将按照LIFO后进先出的顺序添加和弹出元素,会得到DFS算法
function depth_first_search(root, target):
return tree_search(new Stack(), root, target)
有了通用的tree_search模板,我们可以发现BFS和DFS的区别仅在于他们处理元素的顺序。tree_search的初始搜索范围只有root。访问root之后,会将root的所有的子节点添加进sequence,这一步叫做expanding path。随后我们会从sequence取出新的元素,进入下一步搜索。通过向tree_search传入不同的队列结构(Stack/Queue)影响expanding path的过程,而expanding path将决定访问的顺序是DFS还是BFS。
| 算法 | 顺序 | 数据结构 |
|---|---|---|
| DFS深度优先 | LIFO后进先出 | Stack |
| BFS广度优先 | FIFO先进先出 | Queue |
基础知识——图搜索
之前我们说过树是一种特殊的图,树没有环路。如果在树的基础上加上环路,那么就会变成图。与树搜索类似,图搜索也存在有一种通用模板。
我们重新约定节点的结构:每个节点除了包含当前节点的值value,还有一个neighbors列表。与树不同的是,因为图可以有环路,节点甚至可以指向自己,所以节点之间不存在上下级关系。neighbors列表可以包含0个或多个邻居节点。
class Node {
int value;
List<Node> neighbors;
}
假设我们要在图上寻找一个目标节点。我们定义graph_search函数,函数接收起点src、目标节点dst、数据队列sequence。
// 接收起点src、目标节点dst、数据队列sequence
function graph_search(sequence, src, dst):
sequence = {src} // 初始化sequence,并向其中添加起点src
visited = {} // 因为图可以有环路,我们需要一个visited集合来记录已经访问过的节点
while sequence is not empty: // 当sequence中还有元素存在是
curt = sequence.remove() // 从sequence中取出一个元素
if curt in visited: // 避免重复访问
continue
visited.add(curt) // 将curt添加到visited,表示已经访问过
if curt == dst: // 找到目标
return true
for (Node next : curt.neighbors) // 将当前节点相邻的节点添加进sequence
sequence.add(next) // 扩展搜索的范围
return false // 当sequence为空时还没有找到
// 如果将Queue传入graph_search,会得到BFS算法
function breadth_first_search(src, dst):
return graph_search(new Queue(), src, dst)
// 如果将Stack传入graph_search,会得到DFS算法
function depth_first_search(src, dst):
return graph_search(new Stack(), src, dst)
// 如果将PriorityQueue传入tree_search
// sequence将按照每条路径的权重向外扩展节点
// 会得到Uniform-Cost Search算法(Dijkstra算法)
function uniform_cost_search(src, dst):
return tree_search(new PriorityQueue(), src, dst)
图搜索与树搜索基本相同,仅仅由于图可能存在环路,所以我们需要额外的visited集合记录访问过的节点。同样我们通过向graph_search传入不同的队列结构(Stack/Queue/PriorityQueue)影响expanding path的过程,而expanding path将决定访问的顺序为DFS/BFS/UCS。
| 算法 | 顺序 | 数据结构 |
|---|---|---|
| DFS深度优先 | LIFO后进先出 | Stack |
| BFS广度优先 | FIFO先进先出 | Queue |
| UCS一致代价搜索 | 根据权重弹出 | PriorityQueue |
Uniform-Cost Search一致代价搜索算法是Dijkstra算法的变种之一,几乎所有考察Dijkstra算法的面试题都可以用UCS算法来解决。
1.案例: DFS
给定一张图,在图上运行DFS,打印所有节点
思路分析
图上的DFS与树上的DFS算法相似,只需要加入额外的visited集合记录已经访问过的节点,重复访问。
在图上运行DFS的效果如下: 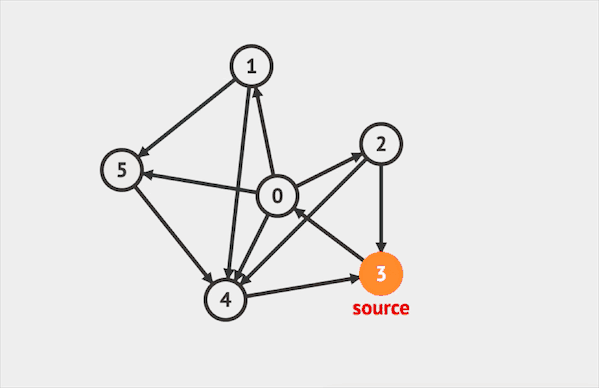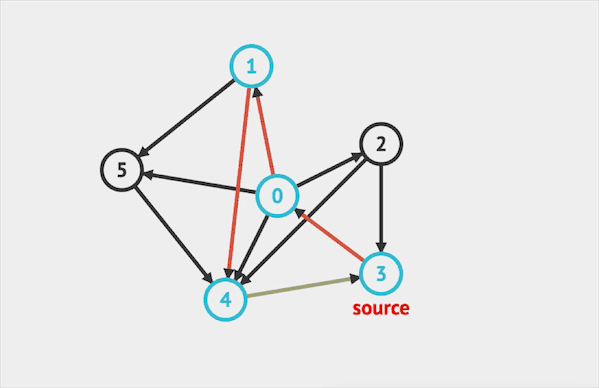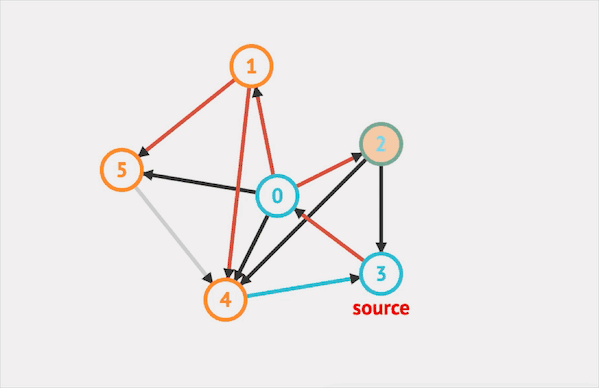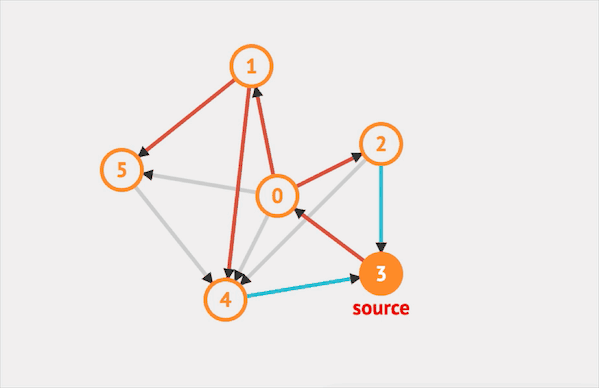 图片由visualgo制作
图片由visualgo制作
代码实现
public List<Node> depthFirstSearch(List<Node> array, Node src) {
// 创建一个Stack作为LIFO队列
Stack<Node> stack = new Stack<>();
// visited集合记录已经访问过的节点
Set<Node> visited = new HashSet<>();
// 从起点src出发
stack.add(src);
while (!stack.isEmpty()) {
// 从LIFO队列中取出一个元素
Node current = stack.pop();
// 避免重复访问
if (visited.contains(current))
continue;
array.add(current);
// expanding path: 将当前节点相邻的节点添加进LIFO队列
for (Node next : current.neighbors)
stack.push(next);
}
return array;
}
分析
时间复杂度O(v+e),空间复杂度O(v),v代表节点个数,e代表边的个数。每个节点仅访问一次所以Stack和Set的空间消耗为O(v)。每条边可能访问一次,时间复杂度O(v+e)。
2.案例: BFS
给定一张图,在图上运行BFS,打印所有节点
思路分析
图上的BFS与树上的BFS算法相似,只需要加入额外的visited集合记录已经访问过的节点,重复访问。
在图上运行BFS的效果如下: 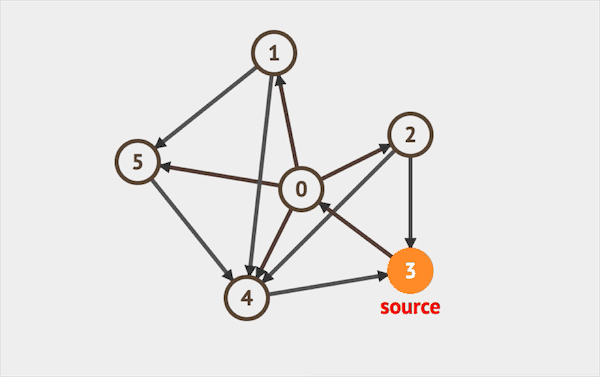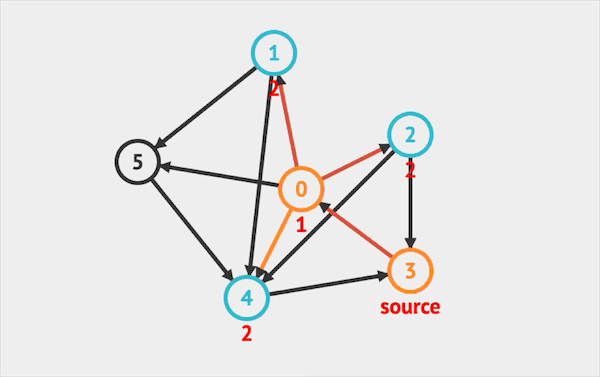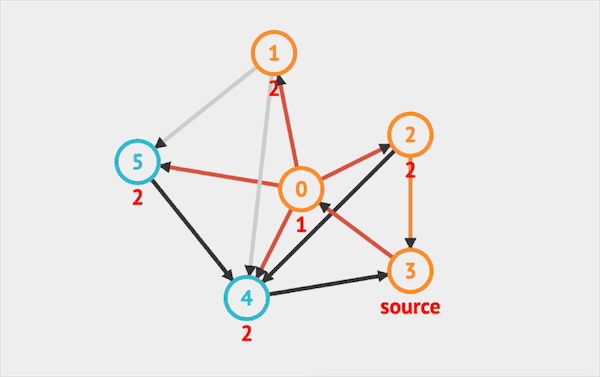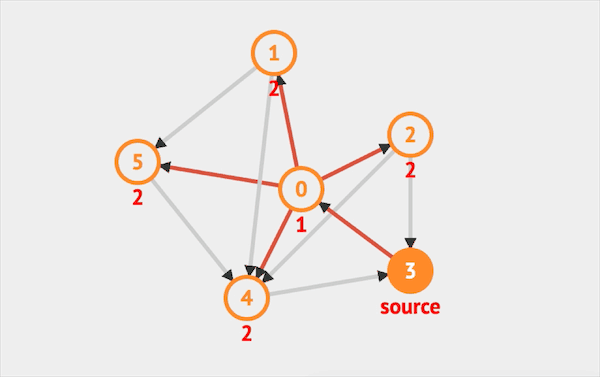 图片由visualgo制作
图片由visualgo制作
代码实现
public List<Node> breadthFirstSearch(List<Node> array, Node src) {
// 创建一个Queue作为FIFO队列
Queue<Node> queue = new LinkedList<>();
// visited集合记录已经访问过的节点
Set<Node> visited = new HashSet<>();
// 从起点src出发
queue.offer(src);
while (!queue.isEmpty()) {
// 从FIFO队列中取出一个元素
Node current = queue.poll();
// 避免重复访问
if (visited.contains(current))
continue;
array.add(current);
// expanding path: 将当前节点相邻的节点添加进FIFO队列
for (Node next : current.neighbors)
queue.offer(next);
}
return array;
}
分析
时间复杂度O(v+e),空间复杂度O(v),v代表节点个数,e代表边的个数。每个节点仅访问一次所以Queue和Set的空间消耗为O(v)。每条边可能访问一次,时间复杂度O(v+e)。
UCS(Dijkstra)算法适用于有权重的图。在没有权重时,每条边权重为1,UCS(Dijkstra)算法退化成BFS算法(PriorityQueue中权重相等,按照元素加入的顺序弹出,退化成Queue)。
总结
本节课我们对比了树和图的概念,总结了树搜索通用算法模板和图搜索通用算法模板,统一DFS和BFS算法。本质上这些不同的遍历方式都符合图遍历的定义,唯一的区别在于使用不同的队列导致expending path的顺序有所不同。