Day 25 Combination 组合问题
之前我们学的章节都是关注于某种特定的数据结构:链表、树、图、堆等等。本章我们将学习数论一类的算法题。这类算法题的题目描述一般比较抽象,需要我们从题干中分析出我们需要的数据结构与算,然后分析出算法逻辑,并且写代码实现。这类题对面试者的逻辑思维能力要求较高,需要面试人员有扎实的代码基础和一定的数学分析能力。
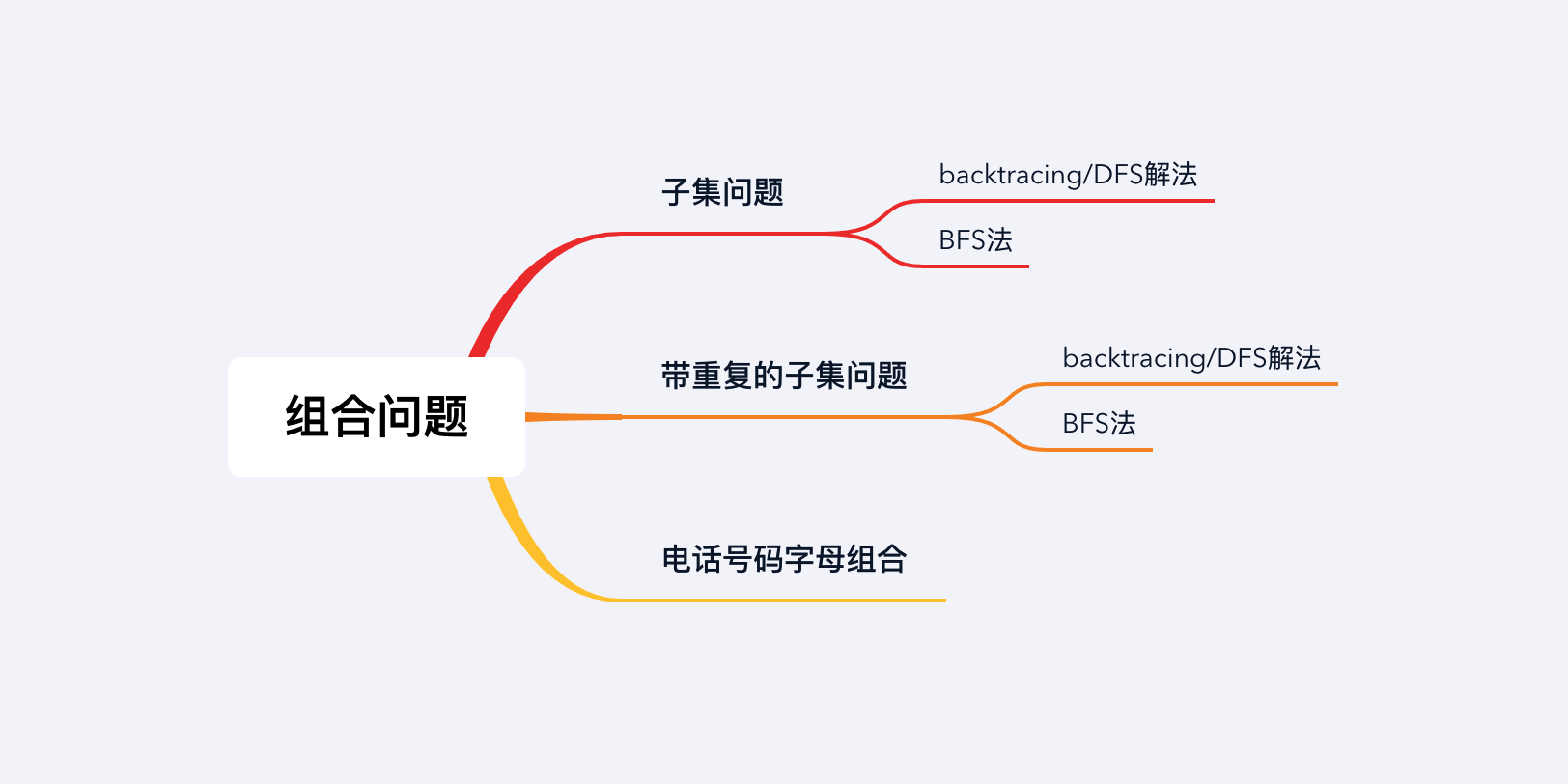
核心算法——组合问题
组合问题一般表述成从n个元素中取出k个元素,可选的组合数量为Cnk。组合问题一般不考虑元素的顺序。在算法题中,组合问题一般会表述成子集问题:给定n个元素,取出包含k个元素的子集。
1.案例: 子集问题
给定一个组整数,返回其所有的子集。
输入: [1, 3] 输出: [], [1], [3], [1,3]
思路分析1
子集问题有多种解法,最通用的解法是回溯法。backtracing回溯法是DFS的变种算法,可以用在所有排列组合类的问题上,是排列组合的通用解法。
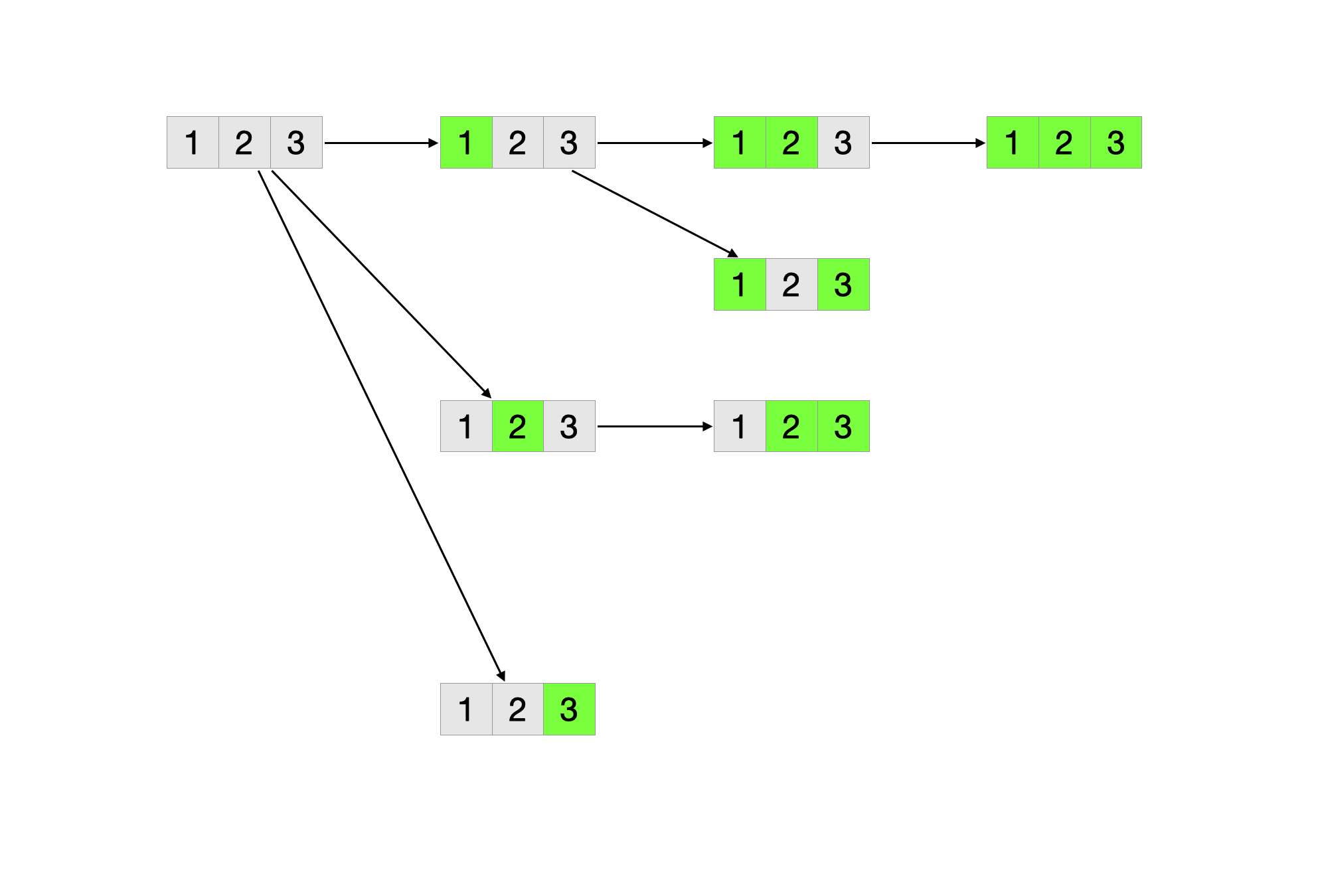
使用backtracing/DFS解题:从空集合开始,将有效的子集加入最终答案。每次遍历所有可能的元素,选择一个加入当前子集。然后递归的调用dfs。
代码实现1
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> res = new ArrayList<>();
dfs(nums, 0, res, ans);
return ans;
}
void dfs(int[] nums, int idx, List<Integer> res, List<List<Integer>> ans) {
// 将有效的子集加入最终答案
ans.add(new ArrayList<>(res));
// 遍历所有可能的元素
for (int i = idx; i < nums.length; i++) {
// 将元素加入当前子集的开头
res.add(nums[i]);
// 递归的调用dfs
dfs(nums, i + 1, res, ans);
// 移除该元素,回溯状态
res.remove(res.size() - 1);
}
}
思路分析2
除了backtracing/DFS法,BFS也可以解决本题。从空集开始,遍历原数组,每次添加一个元素进入已有的集合。
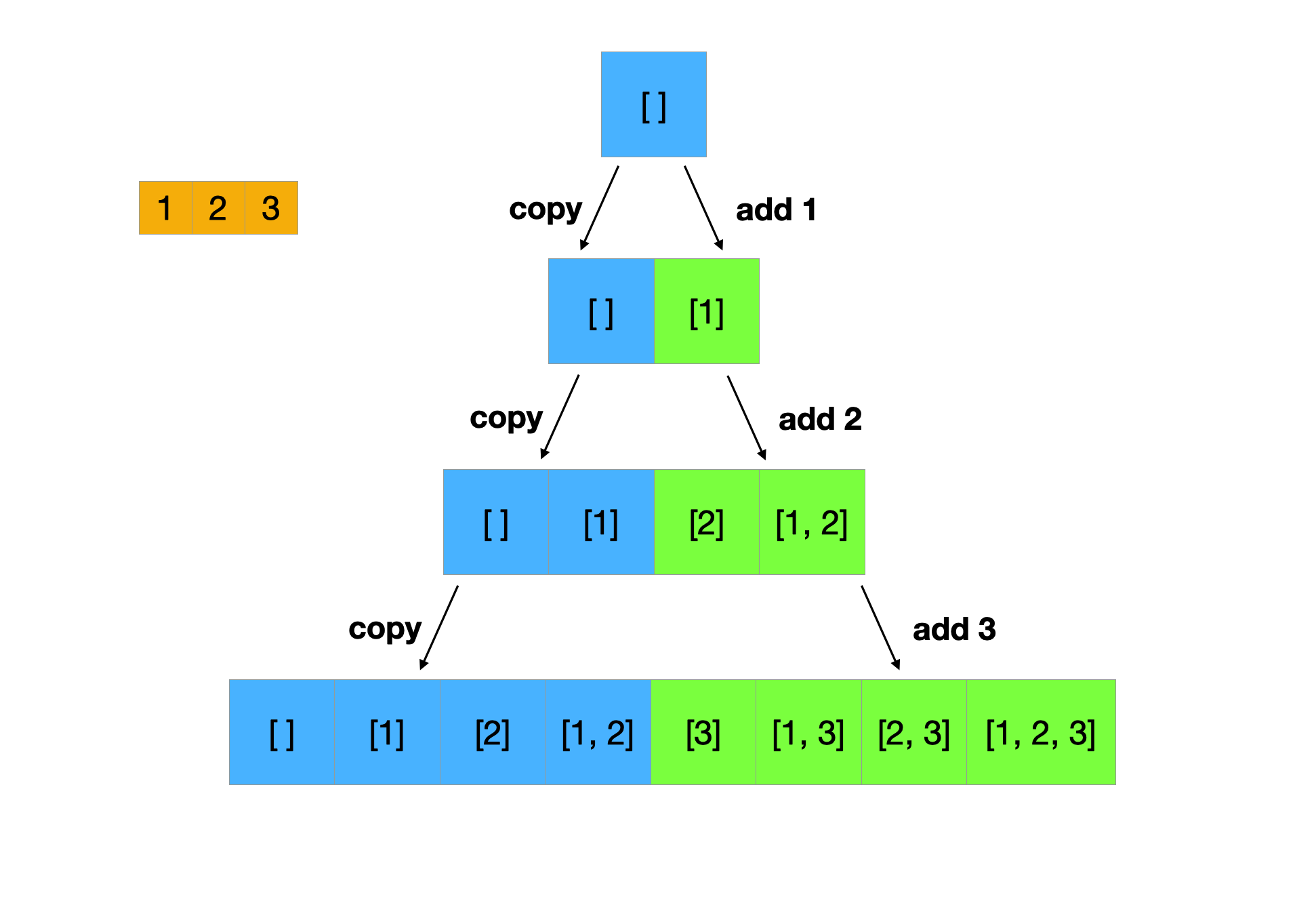
假设给定的集合为[1, 2, 3]:
- 初始空集[]
- 复制已有的集合,并添加元素1,得到[[], [1]]
- 复制已有的集合,并添加元素2,得到[[], [1], [2], [1, 2]]
- 复制已有的集合,并添加元素3,得到[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
代码实现2
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
// 添加初始空集
ans.add(new ArrayList<>());
// 遍历原数组,每次添加一个元素进入已有的集合
for (int n : nums) {
int size = ans.size();
for (int i = 0 ; i < size; i++) {
// 复制已有的集合
List<Integer> copy = new ArrayList<>(ans.get(i));
// 添加元素
copy.add(n);
// 将新的集合加入答案
ans.add(copy);
}
}
return ans;
}
分析
时间复杂度O(n * 2n),空间复杂度O(n * 2n)。组合问题的规模根据输入大小,成指数增长。
2.案例: 子集问题2
给定一个组可能重复的整数,返回其所有的子集。
输入: [1, 5, 3, 3] 输出: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3], [3,3], [1,3,3], [3,3,5], [1,5,3,3]
思路分析1
本题与上一题相似,但是加入了重复元素。作为排列组合的通用解法,回溯法只需要加入一行判断就可以解决这种情况。
- 将给出的数组排序
- 从空集合开始,将有效的子集加入最终答案。
- 每次遍历所有可能的元素,如果当前元素与前一位元素相同,直接跳过当前元素,避免重复子集。选择一个元素加入当前子集。
- 递归的调用dfs。
代码实现1
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 排序数组
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList<>();
List<Integer> res = new ArrayList<>();
dfs(nums, 0, res, ans);
return ans;
}
void dfs(int[] nums, int idx, List<Integer> res, List<List<Integer>> ans) {
// 将有效的子集加入最终答案
ans.add(new ArrayList<>(res));
// 遍历所有可能的元素
for (int i = idx; i < nums.length; i++) {
// 当前元素与前一位元素相同,直接跳过当前元素,避免重复子集
if (i != idx && nums[i] == nums[i-1]) {
continue;
}
// 将元素加入当前子集的开头
res.add(nums[i]);
// 递归的调用dfs
dfs(nums, i + 1, res, ans);
// 移除该元素,回溯状态
res.remove(res.size() - 1);
}
}
思路分析2
不同于backtracing法,BFS虽然也可以解决本题,但是需要做更多的修改来处理重复。
将原数组排序。然后从空集开始,遍历原数组。如果是新的元素,添加元素进入已有的集合。如果是重复的元素,添加元素进入上一步新创建的集合。
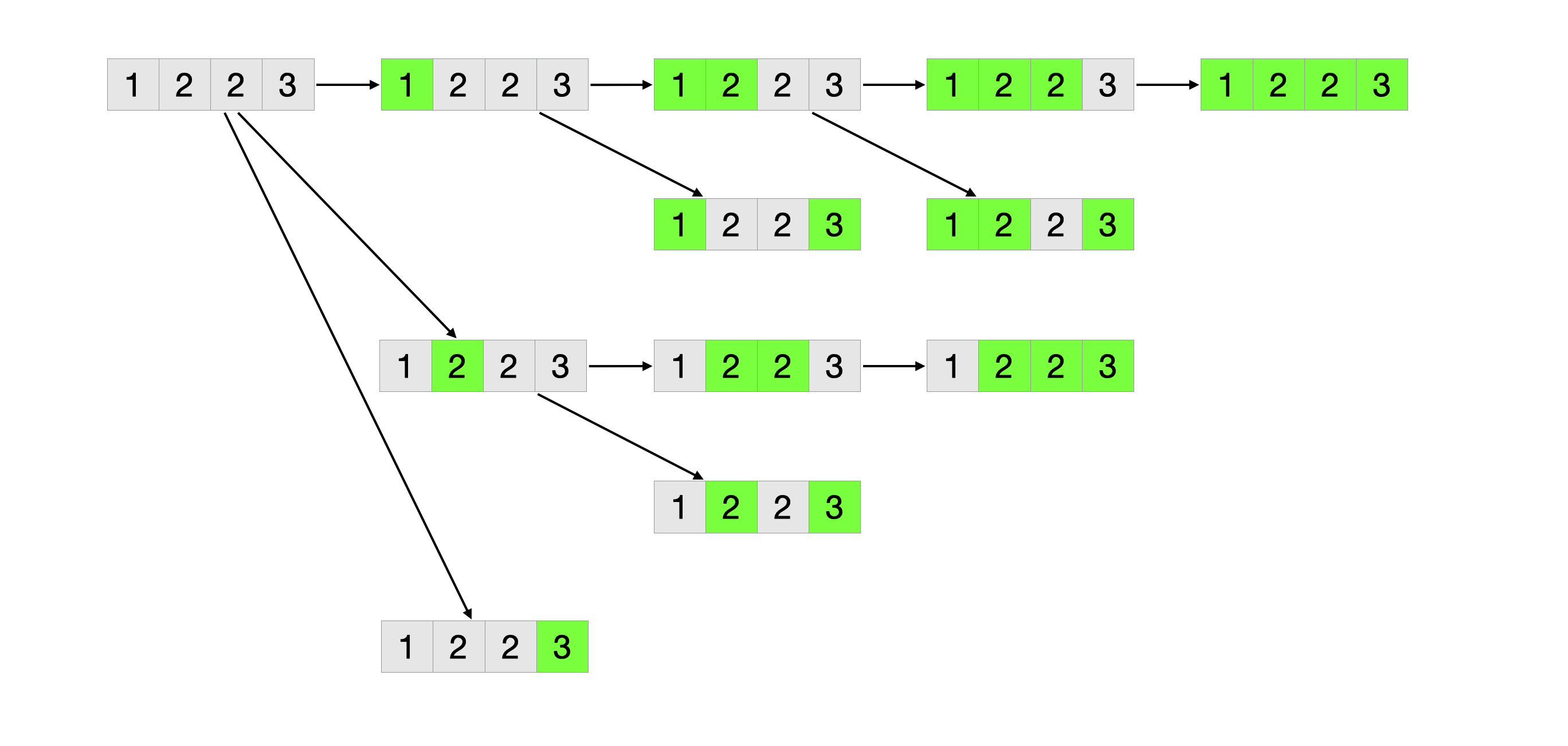
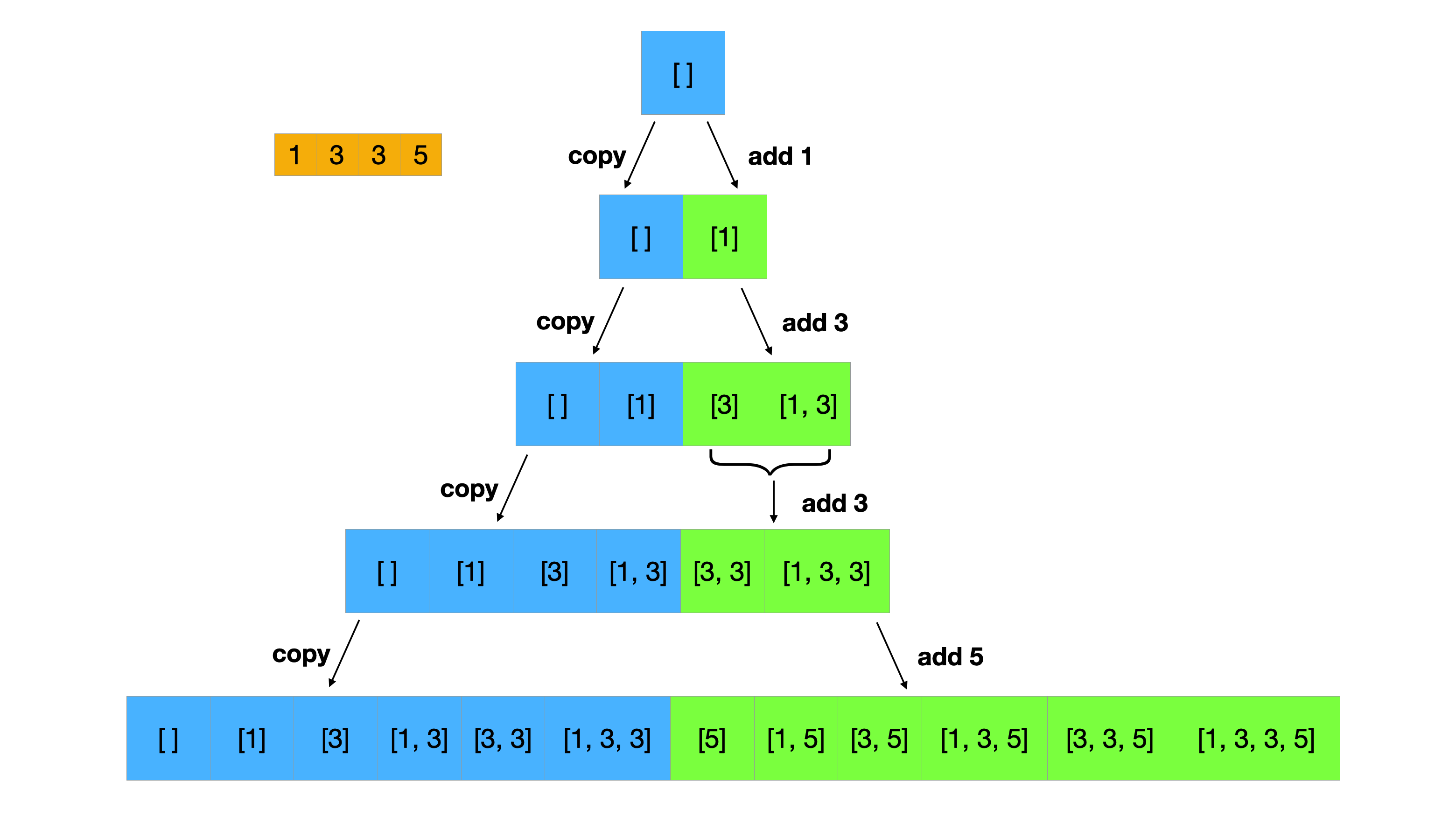
假设给定的集合为[1, 5, 3, 3]:
- 将原数组排序[1, 3, 3, 5]
- 初始空集[]
- 复制已有的集合,并添加元素1,得到[[], [1]]
- 复制已有的集合,并添加元素3,得到[[], [1], [3], [1, 3]]
- 复制已有的集合,并添加元素3到上一步创建的集合,得到[[], [1], [3], [1, 3], [3, 3], [1, 3, 3]]
- 复制已有的集合,并添加元素5,得到[[], [1], [3], [1, 3], [3, 3], [1, 3, 3], [5], [1, 5], [3, 5], [1, 3, 5], [3, 3, 5], [1, 3, 3, 5]]
代码实现2
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 排序数组
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList<>();
// 添加初始空集
ans.add(new ArrayList<>());
int start = 0, end = 1;
// 遍历原数组,每次添加一个元素
for (int i = 0; i < nums.length; i++) {
// start指向所有元素的首位
start = 0;
// 当前元素与前一位元素相同
if (i != 0 && nums[i] == nums[i-1]) {
// start指向上一步创建的集合
start = end;
}
// end指向所有元素的末位
end = ans.size();
for (int j = start; j < end; j++) {
// 复制已有的集合
List<Integer> copy = new ArrayList<>(ans.get(j));
// 添加元素
copy.add(nums[i]);
// 将新的集合加入答案
ans.add(copy);
}
}
return ans;
}
分析
时间复杂度O(n * 2n),空间复杂度O(n * 2n)。组合问题的规模根据输入大小,成指数增长。
3.案例: 电话号码的字母组合
给一个不包含0和1的数字字符串,按照电话按键每个数字代表一个字母,请返回其所有可能的字母组合。
输入: 3 输出: [“d”, “e”, “f”]
电话按键:
| 1 | 2 ABC | 3 DEF |
|---|---|---|
| 4 GHI | 5 JKL | 6 MNO |
| 7 PQRS | 8 TUV | 9 WXYZ |
| * | 0 | # |
思路分析
本题是组合问题的变种题(虽然题目叫做电话字母组合,但是并没有什么真正的组合在里面)。我们需要修改backtracing/DFS算法,而不是生硬地套用模板。
- 如果输入的数字串为空,返回空列表
- 存储各个数字对应的字母
- 对数字串逐位找出可以选用的每个字母,分别递归调用dfs
- 当前位置达到数字串末尾时,将current添加到答案集合,回溯
代码实现
public List<String> letterCombinations(String digits) {
// 建立数字到字母的映射
String[] board = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
List<String> ans = new ArrayList<>();
// 输入的数字串为空,返回空列表
if (digits.length() == 0) {
return ans;
}
dfs(0, "", digits, board, ans);
return ans;
}
void dfs(int idx, String curt, String digits, String[] board, List<String> ans){
// 当前位置达到数字串末尾时,将current添加到答案集合
if (idx == digits.length()) {
ans.add(curt);
return;
}
// 找出可以选用的每个字母,分别递归调用dfs
int d = digits.charAt(idx) - '0';
for (char c : board[d].toCharArray()) {
dfs(idx + 1, curt + c, digits, board, ans);
}
}
分析
时间复杂度O(4n),空间复杂度O(4n)。每个数字最多对应4个可能的字母。
总结
组合问题是数论类题目中最基础的一种。从本章的题目我们可以看出,对于数论类问题,大多数题目仅仅是以数学理论作为题目背景。题目本身依然是围绕DFS/BFS等基础算法出题。因此,对于面试时遇上数论题题目不需要过度紧张。解决这类题目不需要过于高深的数学知识,而是需要扎实的代码基础。