Day 20 - Graph 图 4
上一章我们学习了图类题中的经典考察模板:拓扑排序。拓扑排序与BFS层级遍历算法非常相似,但是思路并不相同。希望读者能够掌握并区分这两种算法。本章我们来看另一种经典考察模板:并查集
核心算法——并查集
并查集本身是一种树型的数据结构(也叫disjoint-set),专门处理连通性(合并与查询)问题。Union-Find并查描述的是该数据结构的算法操作:
- Find:确定元素属于哪一个子集
- Union:将两个子集合并成一个集合
并查集森林
并查集森林是一种将每一个集合以树表示的数据结构,其中每一个节点保存着到它的父节点的引用。在并查集森林中,每个集合的代表即是集合的根节点。Find根据其父节点的引用向根行进,直到到达树根。Union通过将一棵树的根连接到另一棵树的根,将两棵树合并到一起。
Union
Union可以将两个子集合并成一个集合。初始时有4个节点,互不相连。我们先合并1和2,再合并2和3。我们可以发现1和3也被我们间接相连了。

图片由visualgo制作
Find
Find函数用于确定元素属于哪一个子集。比如我们查询集合3,并查集会返回根节点1,说明集合3属于集合1代表的集合。 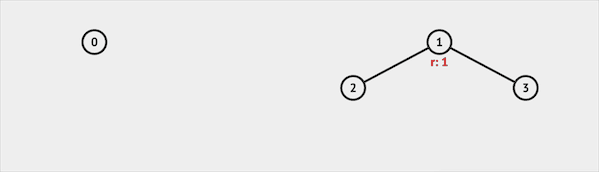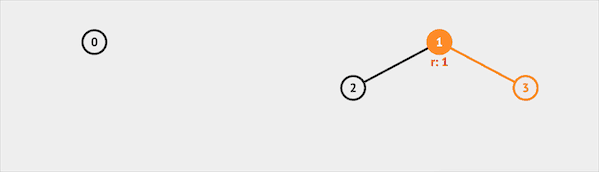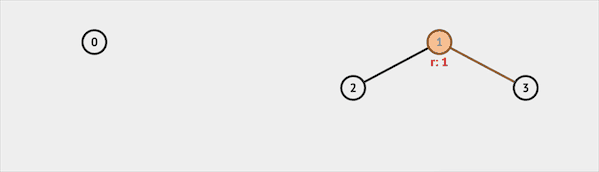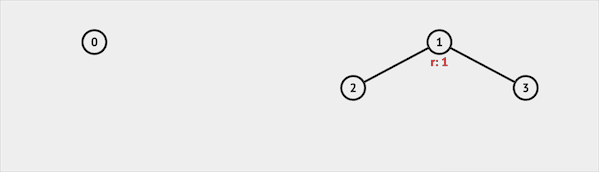
图片由visualgo制作
IsSame
IsSame并不是标准API的一部分,需要自己实现。实现时IsSame函数会调用Find函数,查询两个集合是否属于同一个更大的集合。 比如我们查询IsSame(2, 3),并查集会先查询得知集合2属于集合1代表的集合,集合3也属于集合1代表的集合。返回true,说明集合2 & 3属于同一集合。 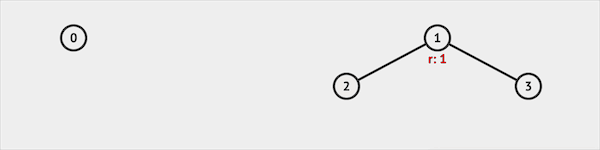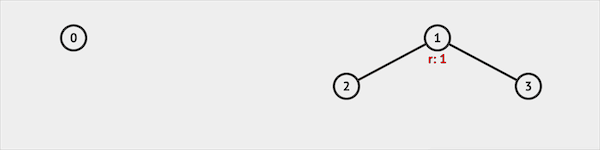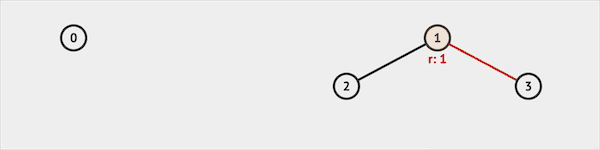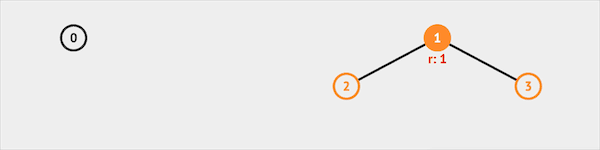
图片由visualgo制作
如果我们查询IsSame(0, 3),并查集会先查询得知集合0属于集合0代表的集合,集合3属于集合1代表的集合。返回false,说明集合0 & 3属于不同集合。 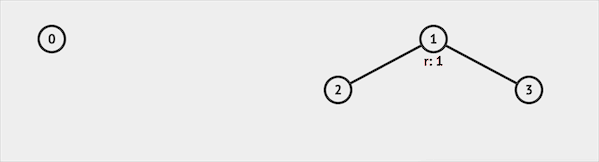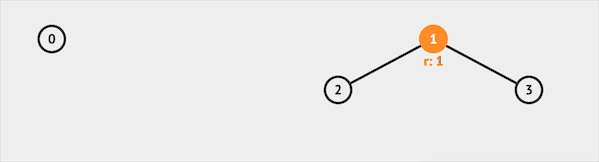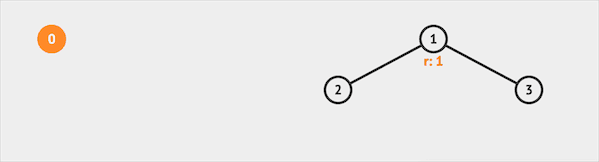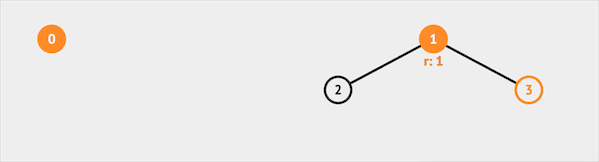
图片由visualgo制作
核心算法——并查集的最优实现
并查集有多种实现方式,我们在这里只介绍并查集的最优实现。这种实现方法能够在不明显增加空间复杂度的情况下,提供最高效的合并、查找功能,并且能适应所有面试题。
class UF {
int count; // 记录当前包含集合的个数
int[] size; // 记录每个集合的大小
int[] id; // 每一个节点保存着到它的父节点的引用
public UF (int n) {
// 初始时,每个节点是只包含它本身的集合
count = n; // n个节点对应n个集合
// 创建与节点个数相同大小的两个数组
size = new int[n];
id = new int[n];
for (int i = 0 ; i < n; i++) {
// 因为每个初始集合是只包含节点本身
size[i] = 1; // 集合大小为1
id[i] = i; // 集合id为节点本身的id
}
}
public int find(int n) {
// 根据当前节点父节点的引用向根行进,直到到达树根
while (n != id[n]) {
id[n] = id[id[n]]; // 路径压缩,改变每一个节点的引用
n = id[n];
}
return n;
}
public boolean union(int a, int b) {
// 分别找到a, b的父节点
int pa = find(a);
int pb = find(b);
// a & b已经属于统一集合
if (pa == pb) return false;
// 将小的集合合并入大的集合
if (size[pa] < size[pb]) {
id[pa] = pb;
size[pb] += size[pa];
} else {
id[pb] = pa;
size[pa] += size[pb];
}
count--; // 合并后,集合个数减1
return true; // 合并成功
}
}
每次操作的时间复杂度可近似看做O(1),空间复杂度O(n)。
1.案例: 冗余的连接
树是一个无环无向联通图。给定一个具有N个节点的树,树上添加了一条额外的边。找到应该被删除的边,将图还原成一棵树。
输入: [[1,2], [1,3], [2,3]] 输出: [2,3]
思路分析
此题的思路比较简单,是并查集的简单应用。样例输入为[[1,2], [1,3], [2,3]]时,给出的图是个环。我们不断地把边加入并查集中,一旦发现有条边的两个端点已经在同一个集合内,说明这两个点之前已经连接过,因此当前这条边就是多余的边。
代码实现
class Solution {
public int[] findRedundantConnection(int[][] edges) {
// 建立一个大小为N的并查集
UF uf = new UF(edges.length + 1);
// 不断地把边加入并查集
for (int[] e: edges) {
// 如果两个端点已经在同一个集合内,这条边就是多余的边
if (!uf.union(e[0], e[1])) {
return e;
}
}
return new int[0];
}
// 将并查集作为inner class,放在原有的class内部
class UF {
int count; // 记录当前包含集合的个数
int[] size; // 记录每个集合的大小
int[] id; // 每一个节点保存着到它的父节点的引用
public UF (int n) {
// 初始时,每个节点是只包含它本身的集合
count = n; // n个节点对应n个集合
// 创建与节点个数相同大小的两个数组
size = new int[n];
id = new int[n];
for (int i = 0 ; i < n; i++) {
// 因为每个初始集合是只包含节点本身
size[i] = 1; // 集合大小为1
id[i] = i; // 集合id为节点本身的id
}
}
public int find(int n) {
// 根据当前节点父节点的引用向根行进,直到到达树根
while (n != id[n]) {
id[n] = id[id[n]]; // 路径压缩,改变每一个节点的引用
n = id[n];
}
return n;
}
public boolean union(int a, int b) {
// 分别找到a, b的父节点
int pa = find(a);
int pb = find(b);
// a & b已经属于统一集合
if (pa == pb) return false;
// 将小的集合合并入大的集合
if (size[pa] < size[pb]) {
id[pa] = pb;
size[pb] += size[pa];
} else {
id[pb] = pa;
size[pa] += size[pb];
}
count--; // 合并后,集合个数减1
return true; // 合并成功
}
}
}
分析
时间复杂度O(n),空间复杂度O(n)。在之后的题解中,我们将略过UF并查集的class定义,直接调用。
2.案例: 岛屿的个数2
给定一个n x m的二维矩阵和一个大小为k的二元数组A,初始二维矩阵全0。二元数组A内的k个元素代表k次操作,表示把二维矩阵中下标为(A[0], A[1])的元素由海洋变为岛屿。返回每次变化之后,二维矩阵中岛屿的数量。
输入: n = 4, m = 5, A = [[1,1],[0,1],[3,3],[3,4]] 输出: [1,1,2,2]
思路分析
因为相邻的岛屿会被看成一个岛屿,所以由海洋变为岛屿可以导致岛屿合并,从而岛屿数量减少。记录岛屿数量变化的过程,我们需要定义一个矩阵记录地图状态, 还需要定义初始含n × m个集合的并查集。不同于上一题,本题是一个二维的空间状态,所以每个节点相邻点有4个方向。我们有两种处理方法:1. 修改并查集的定义,使用二维数组版本的并查集。2. 将二维的位置投影到一维(x, y) -> x * len + y。本题两种方法都可以,方法2代码量较少。
代码实现
public List<Integer> numIslands2(int m, int n, int[][] positions) {
List<Integer> ans = new ArrayList<>();
// 定义一个二维数组来记录岛屿的变化
int[][] island = new int[m][n];
// 记录总共的水域面积
int total = m * n;
// 根据格子的数量创建并查集
UF uf = new UF(total);
// 四个方向
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};
for (int[] p : positions) {
// 如果当前位置可以从海洋变成岛屿
if (island[p[0]][p[1]] != 1) {
// 将当前位置标记成岛屿
island[p[0]][p[1]] = 1;
// 海洋范围减少
total--;
for (int i = 0 ; i < 4; i++) {
// 找到相邻的位置
int x = p[0] + dx[i], y = p[1] + dy[i];
// 如果该位置有效且已经是岛屿,那么与当前岛屿合并
if (x >= 0 && y >= 0 && x < m && y < n && island[x][y] == 1)
uf.union(p[0] * n + p[1], x * n + y);
}
}
// 岛屿的个数等于从所有集合数量中减去海洋的数量
ans.add(uf.count - total);
}
return ans;
}
分析
时间复杂度O(k),空间复杂度O(n * m)
3.案例: 账户合并
给定一个帐户列表,每个元素是一个字符串列表,其中第一位元素是用户名,其余元素是该用户的电子邮件。我们需要合并这些帐户:如果两个帐户有相同的电子邮件地址,则这两个帐户肯定属于同一个人。合并帐户后,按以下格式返回帐户:每个帐户的第一个元素是名称,其余元素是按字典序排序后的电子邮件。
输入: [ [‘Jack’, ‘jacksmith@mail.com’, ‘jack00@mail.com’], [‘Jack’, ‘jacknybravo@mail.com’], [‘Jack’, ‘jacksmith@mail.com’, ‘jack_newyork@mail.com’], [‘Mary’, ‘mary@mail.com’] ] 输出: [ [‘Jack’, ‘jack00@mail.com’, ‘jack_newyork@mail.com’, ‘jacksmith@mail.com’], [‘Jack’, ‘jacknybravo@mail.com’], [‘Mary’, ‘mary@mail.com’] ]
思路分析
本题很明显是连通性问题,但是处理的过程比较复杂。我们将每个账号看做一个单独的节点,然后根据相同的email来连接节点。连接后要将连接在一起的账号放在同一个列表中。
- 将每个email对应到一个账户;如果某个email对应多个账户,用union find将多个账号相连
- 相连之后,并查集会将email汇聚成几个集合,将每个集合和根节点的账号id对应起来,用一个map储存账号id与其该有的所有emails的映射关系。
- 将上一步的列表排序,加上id所对应的人名,加入答案列表
代码实现
public List<List<String>> accountsMerge(List<List<String>> accounts) {
// 创建对应所有账号的并查集
UF uf = new UF(accounts.size());
// 建立一个map,将每个email对应到一个账户
HashMap<String, Integer> email2Id = new HashMap<>();
for (int i = 0; i < accounts.size(); i++) {
List<String> acc = accounts.get(i);
for (int j = 1; j < acc.size(); j++) {
// 每个email对应到第一次出现时所属的账户
String email = acc.get(j);
email2Id.putIfAbsent(email, i);
// 如果对应多个账户,将多个账号相连
uf.union(i, email2Id.get(email));
}
}
// 用一个map储存账号与其该有的emails的映射关系。
HashMap<Integer, List<String>> id2Email = new HashMap<>();
for (String email: email2Id.keySet()) {
// 将每个集合和根节点的账号id对应起来
int id = uf.find(email2Id.get(email));
id2Email.putIfAbsent(id, new ArrayList<>());
id2Email.get(id).add(email);
}
List<List<String>> result = new ArrayList<>();
for (int id : id2Email.keySet()) {
List<String> account = new ArrayList<>();
result.add(account);
// 得到账号用户名
String name = accounts.get(id).get(0);
account.add(name);
// 列表排序
List<String> email = id2Email.get(id);
Collections.sort(email);
// 加入答案列表
account.addAll(email);
}
return result;
}
分析
时间复杂度O(n),空间复杂度O(n)
4.案例: 计算除法
给出一组等式equations和他们对应的值values,每组等式由两个数字组成equations[i] = [Ai, Bi],满足Ai / Bi = values[i]。给出一组queries,每组query由两个数字组成queries[i] = [Ci, Di]。返回所有queries的值。
输入: equations = [[“a”,”b”],[“b”,”c”]] values = [2.0,3.0] queries = [[“a”,”c”],[“b”,”a”],[“a”,”e”],[“a”,”a”],[“x”,”x”]] 输出: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
思路分析
本题的原型是谷歌的一道汇率转换题,题干与本题类似,给出A->B, B->C, C->D… 等汇率转换比率,计算A->D的汇率。
这题需要对UnionFind算法做出一点修改。只有两个节点相连通,才能相除。这说明他们属于同一个集合,有一个共同的父节点。所以我们需要额外的map记录当前节点对它所属的父节点的权重。比如X、Y有共同的父节点Z,我们已知 X/Z 的值和 Y/Z 的值,所以 X/Y = (X/Z) / (Y/Z)。
代码实现
class Solution {
// 记录每个节点对应的父节点
Map<String, String> father = new HashMap<>();
// 记录每个节点对它所属的父节点的权重
Map<String, Double> weight = new HashMap<>();
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
for (int i = 0; i < equations.size(); i++) {
// 获取每个等式的两个部分s1 & s2
String s1 = equations.get(i).get(0), s2 = equations.get(i).get(1);
// 如果s1 & s2没被访问过,将它们加入并查集
putIfAbsent(s1);
putIfAbsent(s2);
// 找到对应的父节点
String root1 = find(s1);
String root2 = find(s2);
// 将root1的父节点指向root2
father.put(root1, root2);
// 更新root1对它所属的父节点的权重
weight.put(root1, weight.get(s2) * values[i] / weight.get(s1));
}
double[] res = new double[queries.size()];
for (int i = 0; i < queries.size(); i++) {
// 获取每个query的两个部分s1 & s2
String s1 = queries.get(i).get(0), s2 = queries.get(i).get(1);
// 如果s1 & s2没在图中出现过,或者不属于同一集合
if (!father.containsKey(s1) || !father.containsKey(s2) || !find(s1).equals(find(s2)))
res[i] = -1.0; // 无效查询,返回-1
else // 根据他们分别对父节点的权重,计算结果
res[i] = weight.get(s1) / weight.get(s2);
}
return res;
}
private void putIfAbsent(String s) {
father.putIfAbsent(s, s);
weight.putIfAbsent(s, 1.0);
}
// 修改后的find函数
private String find(String s) {
// 如果已经到达父节点,返回本身
if (father.get(s).equals(s)) {
return s;
}
// 更新到父节点的权重
String prev = father.get(s);
String p = find(father.get(s));
father.put(s, p);
weight.put(s, weight.get(prev) * weight.get(s));
return p;
}
}
分析
时间复杂度O(n),空间复杂度O(n)。本题可以使用BFS/DFS求解,感兴趣的读者可以作为习题。
总结
本章我们学习了图类题中的第二类经典考察模板:并查集。并查集经常出现在大厂面试题中,本身难度不高,但是需要读者掌握这种数据结构的写法。大部分题目都只是并查集结构的简单应用。
习题
- 使用BFS/DFS求解案例4计算除法