Day 12 - Stack 栈
本章我们来学习三种队列类的数据结构:Stack栈、Queue队列、Heap堆。这三种结构的相关性并不体现在代码上,而体现在逻辑层面和使用层面。他们都可以加入一个元素,移除一个元素,访问但不删除下一个元素。简单来说,Stack、Queue、Heap可以被看做三种不同的队列:Stack是后进先出队列,Queue是先进先出队列,Heap是按照优先级排列的队列。(这里为了避免队列这个词出现歧义,我用Queue表示先进先出的数据结构,用队列表示数据加入/删除的顺序结合)
这三种结构经常被拿来作比较,通常在教科书中会被看做三个不同的考点。但是在面试时,这三种结构可以被放在图论这个大类下,在某些情况下甚至可以出现在同一题里。Stack栈、Queue队列、Heap堆是必须要掌握的数据结构。
基础知识——栈
Stack 栈可以看做是一种特殊的线性表,所有的操作(访问、插入、删除)只能在栈顶进行,按照后进先出(LIFO, Last In First Out)的顺序运作。所以使用ArrayList实现栈比使用LinkedList实现更加高效。在Java中,Stack的实现是基于Vector类,而Vector类的写法类似于ArrayList。
Stack的主要API有三个:push插入, pop删除, peek访问。
- push只能将元素插入栈顶。
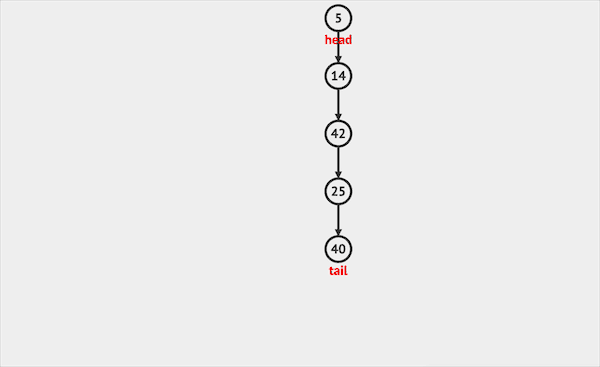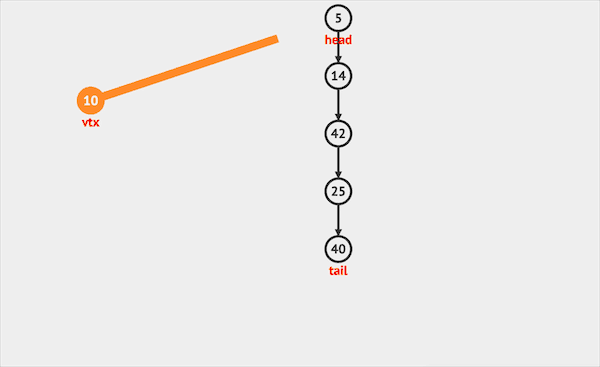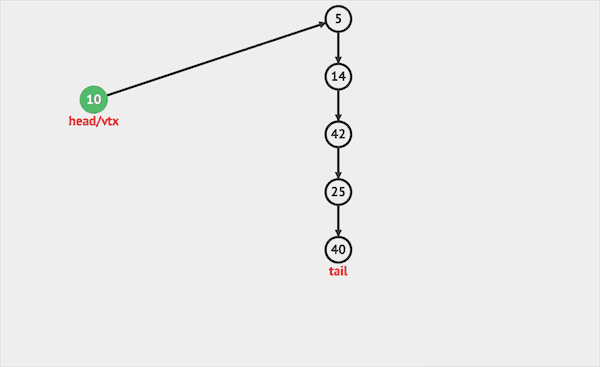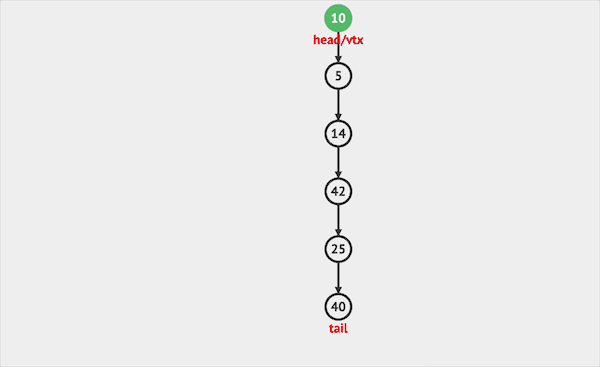
图片由visualgo制作
- pop只能将栈顶元素移除。
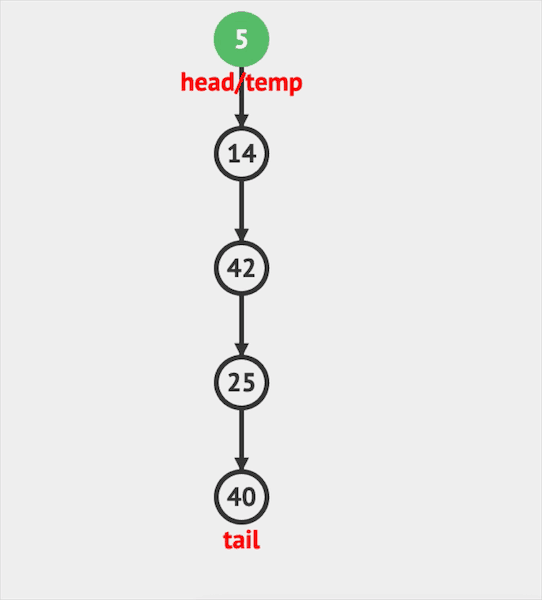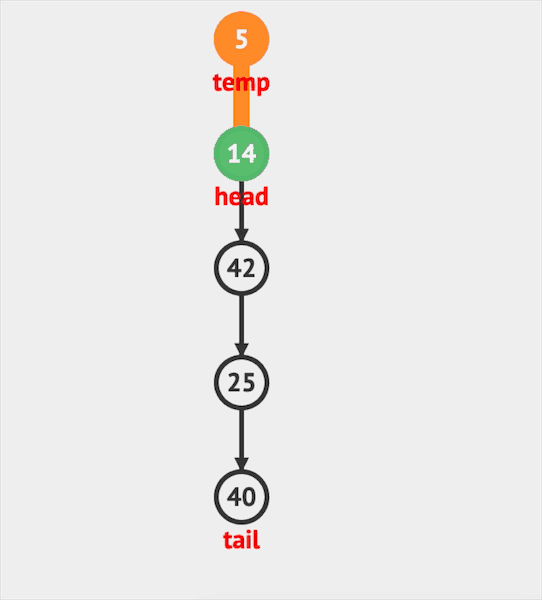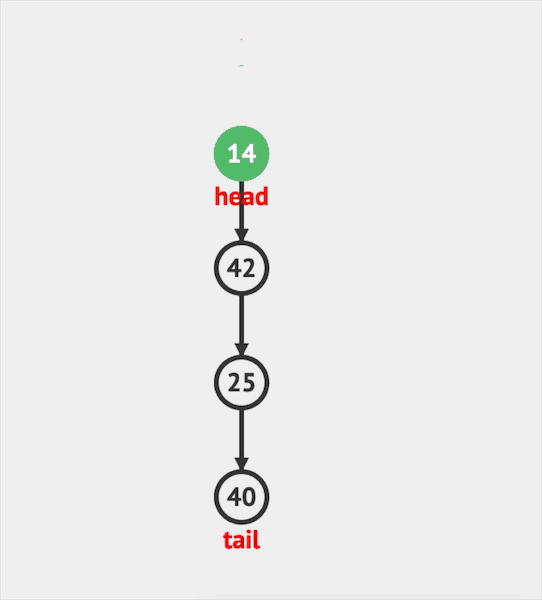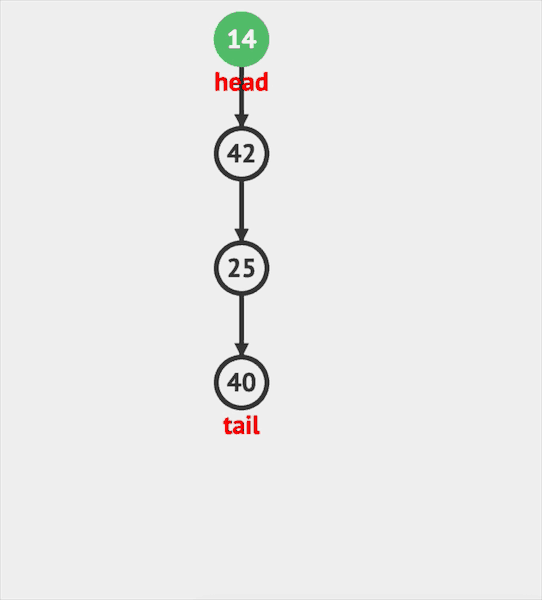
图片由visualgo制作
- peek访问返回栈顶元素,但是不删除。
1.案例: 有效的括号序列
给定一个字符串所表示的括号序列,包含以下字符: ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[’ , ‘]’,判定是否是有效的括号序列。括号必须依照”()”顺序表示,”()[]{}”是有效的括号,”([)]”是无效的括号。
输入:string = “([])(){}(())()()” 输出: true
思路分析
这道题是Stack的基础运用。输入是一个string,在本题中它相当于一个char数组。输入的范围仅包括有效的括号字符: ( , ) , { , } , [ , ] . 为了判断输入的括号序列是否有效,我们需要确保每一个开括号都对应一个闭括号,并且开括号的顺序和闭括号的顺序相反。
因此我们需要遍历每个字符,如果遇到的是开括号 ( , { , [ ,那么我们将它压栈。如果我们遇到的是闭括号 ) , } , ] ,那么我们需要与前一个开括号进行比较,确保他们成对。对于成功配对的括号,我们可以将他们从栈中删除。否则说明收到的序列不是有效括号序列。
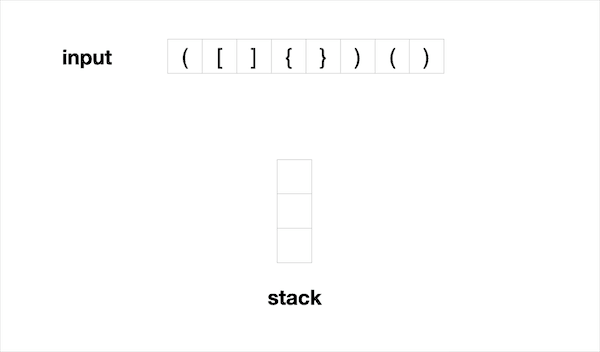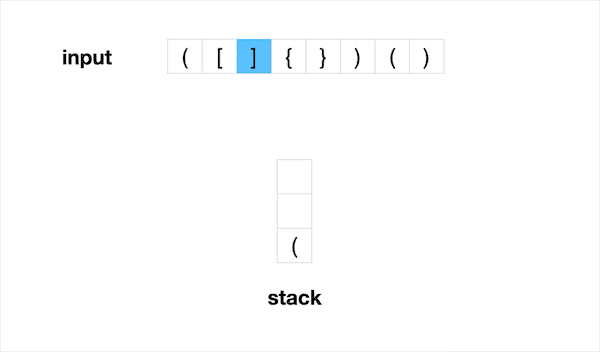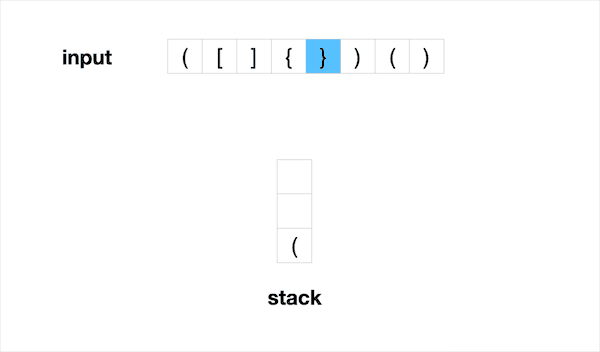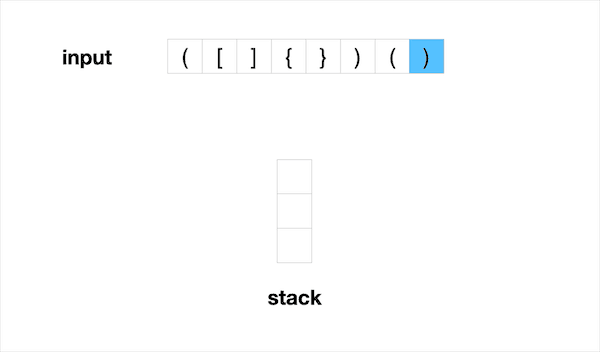
最后如果栈中没有额外的括号留下,那么整个序列是有效括号序列。
代码实现
public boolean isValid(String s) {
// 创建一个栈
Stack<Character> stack = new Stack<>();
// 遍历每一个字符
for (char c : s.toCharArray()) {
// 如果遇到的是开括号,将它压栈
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
}
// 如果遇到的是闭括号 ,需要与前一个开括号进行比较,确保成对
if (c == ')' || c == ']' || c == '}') {
// 确保存在至少一个开括号
// 并且该开括号与当前闭括号成对
// 这里我们利用他们在ASCII码中的位置,快速判断是否成对
if (stack.isEmpty() || Math.abs(stack.pop() - c) > 2) {
return false;
}
}
}
// 如果栈中没有额外的括号留下,那么是有效括号序列。
return stack.isEmpty();
}
分析
时间复杂度O(n),空间复杂度O(n)。我们需要遍历整个输入的string,并且最差情况下需要将所有字符存在栈中。
核心算法——单调栈
Monotone Stack 单调栈,栈内元素都是单调递增或者单调递减的,有时候甚至是严格的单调递增或递减。从单调栈中获取元素,元素满足单调性。单调栈是Stack类考题中最常出现的解题技巧。
2.案例: 最小值最大值操作栈
实现一个栈,要求 O(1) 开销, 支持以下操作:
- push(val) 将 val 压入栈
- pop() 将栈顶元素弹出, 并返回这个弹出的元素
- peek() 获得栈顶元素
- getMin() —— 获得栈中的最小元素。
- getMax() —— 获得栈中的最大元素。
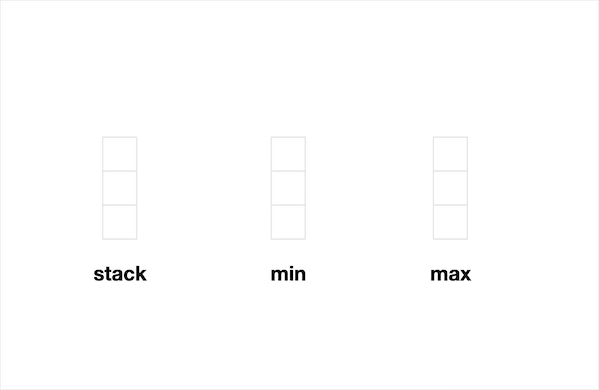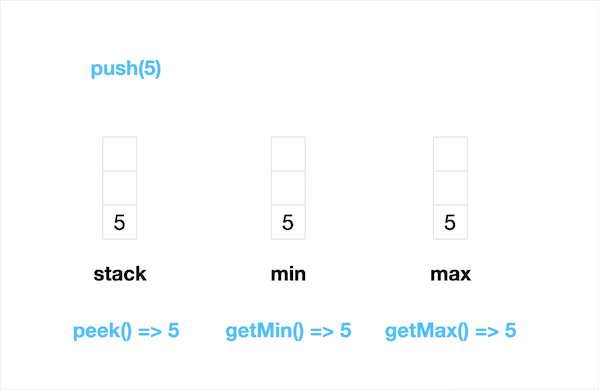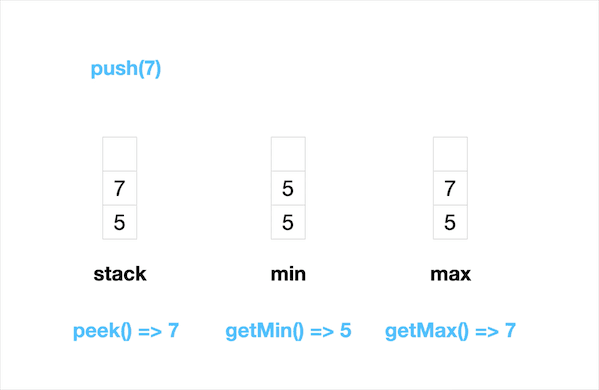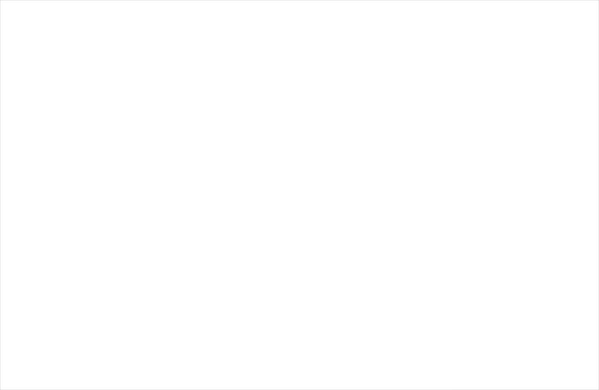
Sample: MinMaxStack(): - push(5): - getMin(): 5 getMax(): 5 peek(): 5 push(7): - getMin(): 5 getMax(): 7 peek(): 7 push(2): - getMin(): 2 getMax(): 7 peek(): 2 pop(): 2 pop(): 7 getMin(): 5 getMax(): 5 peek(): 5
思路分析1
本题是单调栈的经典题型,要求我们实现的栈可以直接读取最大/最小元素。实际上,题目的含义是要求我们实现一个Stack用三个Stack的功能:正常Stack + 单调增Stack + 单调减Stack。
我们可以直接顺着这个思路来解题,初始化三个Stack:一个普通Stack + 两个单调栈(一个维护升序,一个维护降序)。单调升序栈每次只加入比上一个元素更大的元素,单调降序栈每次只加入比上一个元素更小的元素。peek(), getMin(), getMax()分别从三个栈获取栈顶元素。每次push一个新元素入栈时:
- 普通stack直接压栈
- 单调升序栈将当前元素与上一个元素相比较,如果当前元素更大则压栈当前元素,否则复制一份前一个元素
- 单调降序栈将当前元素与上一个元素相比较,如果当前元素更小则压栈当前元素,否则复制一份前一个元素
对于本题而言,单调序列和严格单调序列都可以完成解题,相比之下,非严格单调序列的实现更加简单易懂。
代码实现1
class MinMaxStack {
// 初始化三个Stack:一个普通Stack + 两个单调栈
private Stack<Integer> stack = new Stack<>();
private Stack<Integer> min = new Stack<>();
private Stack<Integer> max = new Stack<>();
public int peek() { // 从普通栈获取栈顶元素
return stack.peek();
}
public int pop() {
int x = stack.pop();
min.pop();
max.pop();
return x;
}
public void push(Integer x) {
// 单调降序栈:如果当前元素更小则压栈当前元素,否则复制前一个元素
min.push(stack.isEmpty() ? x : Math.min(x, min.peek()));
// 单调升序栈:如果当前元素更大则压栈当前元素,否则复制前一个元素
max.push(stack.isEmpty() ? x : Math.max(x, max.peek()));
// 普通stack直接压栈
stack.push(x);
}
public int getMin() { // 从降序栈获取栈顶元素
return min.peek();
}
public int getMax() { // 从升序栈获取栈顶元素
return max.peek();
}
}
思路分析2
解法1存在一个缺陷:随着要求保存的特性越多,需要同时维护的栈越多。本题中只要求增加了获取最大/最小值的操作,我们额外多维护了两个栈。如果题目中加入更多要求:增加获取当前平均值的函数getMean(), 获取当前第三大的值get3rdMax()…这样我们需要同时维护更多的栈。
一个应对的解决方法是只是用一个栈,但是这个栈并不保存数据本身,而是保存一个对象。该对象包含了我们所有需要的特性。一个取巧的方法是使用数组,数组第1位保存当前数值,第2位保存当前最小值,第3位保存当前最大值。我们可以根据需求修改数组,并且只需要维护一个栈。
代码实现2
class MinMaxStack {
// 初始化一个栈
private Stack<int[]> stack = new Stack<>();
public int peek() {
// 数组第1位保存当前数值
return stack.peek()[0];
}
public int pop() {
return stack.pop()[0];
}
public void push(Integer x) {
if (stack.isEmpty()) {
stack.push(new int[]{x, x, x});
return;
}
int[] curt = stack.peek();
// 在压栈时和前一位数值进行比较,构造新的数据对象
stack.push(new int[]{x, Math.min(x, curt[1]), Math.max(x, curt[2])});
}
public int getMin() {
// 数组第2位保存当前最小值
return stack.peek()[1];
}
public int getMax() {
// 数组第3位保存当前最大
return stack.peek()[2];
}
}
分析
时间复杂度O(1),空间复杂度O(1)。每一步操作消耗的时间和空间在数量级上与单个Stack操作一致。
3.案例: 下一个更大的数
有两个数组 nums1和nums2(互不重复),其中nums1是nums2的子集。 在nums2的相应位置找到nums1所有元素的下一个更大数字。nums1中的数字x的下一个更大数字是nums2中x右边第一个更大的数字。 如果它不存在,则为此数字输出-1。
输入: nums1 = [4,1,3], nums2 = [1,3,4,2] 输出: [-1,3,4]
思路分析
本题依旧是单调栈的运用。给定的是一组输入nums1和一组数据集合nums2。要求在nums2中找到每个数字的下一个更大的数,然后按照nums1的顺序输出。
因此我们先针对nums2,利用单调栈来建立每个数字和它下一个更大数的对应关系。再按照nums1的数字输出最终结果。寻找数字x的下一个更大数y,等价于寻找y的前一个稍小的数x。而前一个稍小的数x,其实是在y出现之前的最大值。有了这层对应关系,我们就可以利用之前我们学的单调栈的实现方法。
- 初始化一个Stack作为单调栈。
- 遍历nums2,对于每个数字 2.1. 如果栈顶数字小于当前数字,则当前数字是栈顶数字的下一个更大数。 2.2. 弹出栈顶数字,利用map保存对应关系。跳转到步骤2.1 2.3. 如果栈顶数字大于当前数字,压栈,维护单调性
- 遍历nums1,对于每个数字,在map中寻找对应的下一个更大数,如果不存在则返回-1.
代码实现
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
HashMap<Integer, Integer> map = new HashMap<>();
// 初始化一个Stack作为单调栈。
Stack<Integer> stack = new Stack<>();
for (int n : nums2) { // 遍历nums2
while (!stack.isEmpty() && n > stack.peek()) // 如果栈顶数字小于当前数字
map.put(stack.pop(), n); // 弹出栈顶数字,利用map保存对应关系
stack.push(n); // 如果栈顶数字大于当前数字,压栈
}
int[] ans = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) // 遍历nums1
ans[i] = map.getOrDefault(nums1[i], -1); // 在map中寻找对应的下一个更大数,不存在则返回-1
return ans;
}
分析
时间复杂度O(n),空间复杂度O(n)
总结
这节课我们学习了经典的Stack结构和常见考点单调栈在面试题中的应用。下节课将对比队列与栈的考题。
习题
- 最小值操作栈:实现一个栈,要求 O(1) 开销, 支持以下操作:
- push(val) 将 val 压入栈
- pop() 将栈顶元素弹出, 并返回这个弹出的元素
- peek() 获得栈顶元素
- getMin() —— 获得栈中的最小元素。
- 下一个更大的数2:给出一个循环数组,找到每个元素的下一个更大的数。 如果它不存在,则为此数字输出-1。