Day 04 - Array 数组1
数组是由相同类型的元素的集合所组成的数据结构,物理层面上计算机会分配一块连续的内存来存储这些元素。数组中每个元素在内存中相邻,所有的元素存储在一个连续的内存块中。逻辑层面上,用户可以利用元素的索引可以计算出该元素对应的存储地址。
最简单的数据结构类型是一维数组。它是最简单易学、最广泛使用的数据类型,也是最古老和最重要的数据结构之一。可以说是面试必考,工作必会。
1.案例: 单调数列
判断数组是否具有单调性(单调递增或单调递减)
输入: [-1, -5, -10, -1100, -1100, -1101, -1102, -9001] 输出: true
输入: [1,3,2] 输出: false
思路分析
数组类的题有一部分与本题类似,需要我们比较相邻两个元素。因此我拿这道题作为一道开胃菜,分享给大家体验一下数组类算法题的出题思路。
题目要求我们确定数组是否具有单调性。我们可以先假设数组是单调增的,因此在每个位置A[i] <= A[i + 1]。遍历一遍数组,检查在每一个i是否都有A[i] <= A[i + 1]。类似地,如果数组是单调减的,那么每个位置A[i] >= A[i + 1]。
我们用dec和inc两个flag代表数组的单调性,遍历数组,判断每个位置上是否符合单调性。如果所有位置都符合,那么至少有一个flag始终为true,返回其中一种结果。
代码实现
public boolean isMonotonic(int[] A) {
boolean inc = true, dec = true;
for (int i = 1; i < A.length; i++) {
inc &= A[i-1] <= A[i];
dec &= A[i-1] >= A[i];
}
return inc || dec;
}
分析
时间复杂度O(n),空间复杂度O(1)
2.案例: 数组中的最长山脉
写出一个方法,对于给定的整数数,返回数组中最长山峰的长度
山峰在数组中被定义为:峰顶左侧的值,严格单调增;右侧的值,严格单调减。一个山峰至少要由三个数字组成
输入: [1, 2, 3, 3, 4, 0, 10, 6, 5, -1, -3, 2, 3] 输出: 6
思路分析1
本题要求我们找到一个山峰peak。对于peak而言,向左和向右都是递减的。反过来说,找到两个序列,序列1从左往右递增,序列2从右往左递增,两个序列相交的点就是peak。我们只需要找到所有peak中,两个序列长度和最长的那个。
我们可以通过添加辅助数组的方式,来简化解法。
- 创建一个辅助数组1,从左往右计算每个位置递增序列的长度
- 创建一个辅助数组2,从右往左计算每个位置递增序列的长度
- 在每个位置,将数组1的值和数组2的值相加,和最大的位置即为peak的位置
- 返回最大的和
代码实现1
public int longestMountain(int[] A) {
int[] leftPeak = leftToRight(A); // 从左往右计算
int[] rightPeak = RightToLeft(A); // 从右往左计算
int longest = 0;
for (int i = 0; i < A.length; i++) {
if (leftPeak[i] == 0 || rightPeak[i] == 0) {
continue;
}
longest = Math.max(longest, leftPeak[i] + rightPeak[i] + 1); // 最大的和
}
return longest;
}
两个帮助计算递增序列的辅助函数拥有相同的逻辑
private int[] leftToRight(int[] array) {
int[] ans = new int[array.length];
for (int i = 1; i < ans.length; i++) {
if (array[i] > array[i - 1]) {
ans[i] = ans[i - 1] + 1;
}
}
return ans;
}
private int[] RightToLeft(int[] array) {
int[] ans = new int[array.length];
for (int i = ans.length - 2; i >= 0; i--) {
if (array[i] > array[i + 1]) {
ans[i] = ans[i + 1] + 1;
}
}
return ans;
}
分析
时间复杂度O(n),空间复杂度O(n)
大部分题目都可以通过添加有限个辅助数组来简化难度,这暗示了大部分数组题的空间消耗等价于输入数组的大小。所以一般空间复杂度不超过O(n)。因此对于数组题的优化,大部分只要找到O(1)空间复杂度的解法。
思路分析2
解法1通过添加辅助数组的方式,简化了算法的难度,但是消耗了额外的空间。实际上我们可以只消耗O(1)的空间。我们使用三个指针start, end, peak来指向每个山峰的起点、终点和峰值。通过比较三个指针的位置来判断当前山峰是否符合要求。
假设我们有输入数组nums = [2, 1, 2, 3, 2, 1, 0, 2, 3, 1, 1],我们可以画成下图。在遍历数组的过程中,对于每个山峰,我们记下起点start、终点end和峰值peak的位置。
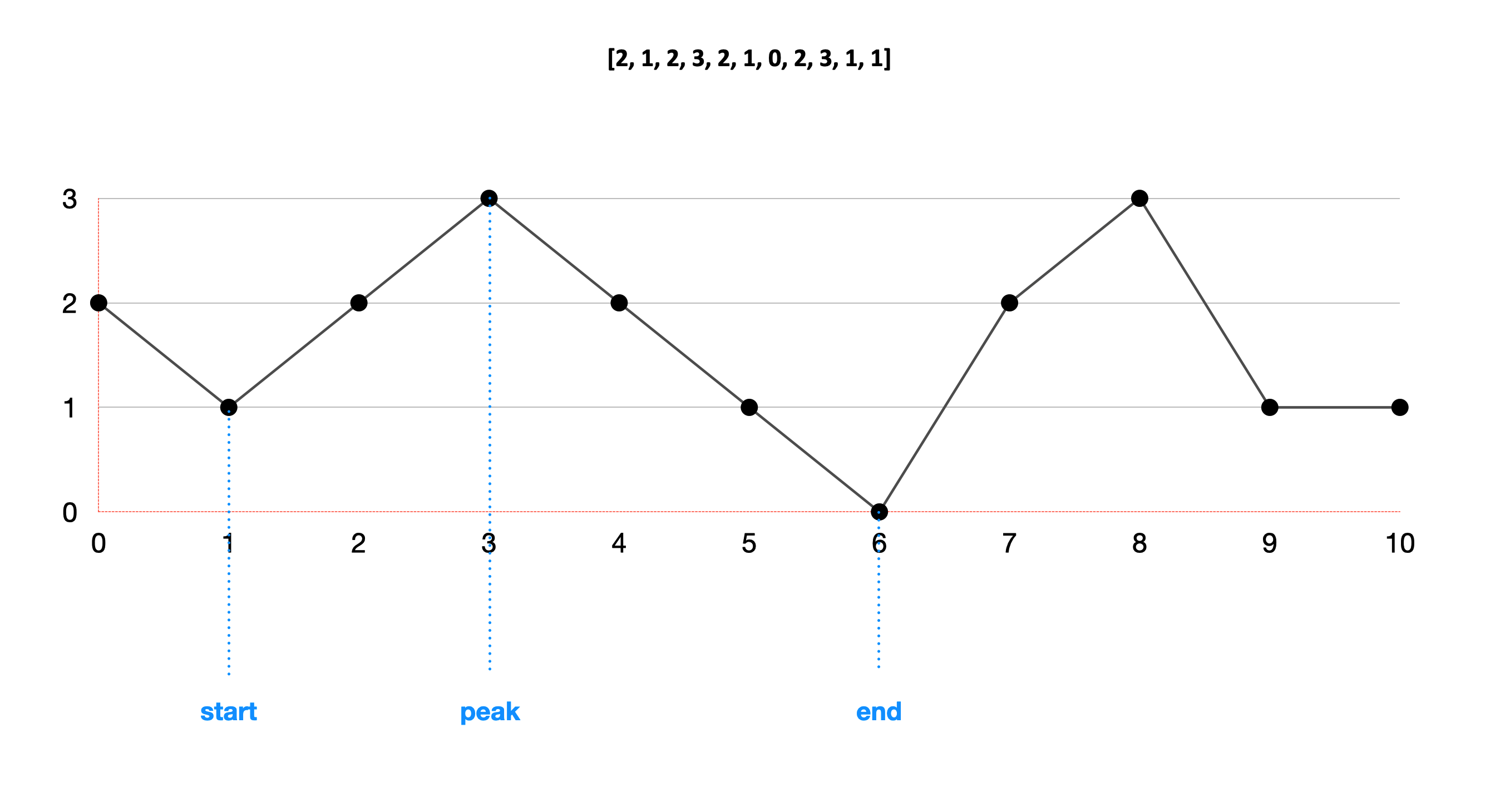
这样我们只需要使用O(1)的额外空间。
代码实现 2
public int longestMountain(int[] A) {
int ans = 0, end = 0;
while (end < A.length) {
int start = end; // 记下起点位置
while (end + 1 < A.length && A[end] < A[end + 1]) // 向上爬,寻找峰值
end++;
int peak = end; // 记下峰值位置
while (end + 1 < A.length && A[end] > A[end + 1]) // 向下走,寻找终点
end++;
if (start < peak && peak < end) // 比较起点、峰值和终点的位置,如果符合条件,记下当前最大值
ans = Math.max(ans, end - start + 1);
if (start == end) // 如果是平坡,将指针向前移动一步,防止死循环
end++;
}
return ans;
}
分析
时间复杂度O(n),空间复杂度O(1)
思路分析3
解法2使用了start, end, peak三根指针。还有一种解法与之类似,但是使用了up和down两个状态,来代替三根指针。通过比较up和down的值来判断当前状态。这里作为解法2的补充,不作为主要解题方法。
代码实现3
public int longestMountain(int[] A) {
int ans = 0, up = 0, down = 0;
for (int i = 1; i < A.length; i++) {
if (down > 0 && A[i - 1] < A[i] || A[i - 1] == A[i]) // 1. 下坡结束,出现上坡 2. 遇到平坡
up = down = 0; // 将之前的记录清零
if (A[i - 1] < A[i]) // 上坡
up++;
if (A[i - 1] > A[i]) // 下坡
down++;
if (up > 0 && down > 0 && up + down + 1 > ans) // 更新当前最大值
ans = up + down + 1;
}
return ans;
}
分析
时间复杂度O(n),空间复杂度O(1)
3.案例: 最小差
给定两个数组,找到一对数字(两个数组各取一个),他们的差值最小。返回这两个数组。
输入: arrayOne = [-1, 5, 10, 20, 28, 3] arrayTwo = [26, 134, 135, 15, 17] 输出: 2
思路分析
我们需要在两个数组里,各取一个数字。这明显暗示了我们需要使用Two Pointers技巧。Two Pointers是数组题的经典考点之一,我们会在下一章深入体会Two Pointers技巧的多种使用方式。本题需要用的Two Pointers技巧的一个变种,根据使用方法通常称为“谁小移谁”(滑稽)。
- 将两个数组分别排序
- 使用两根指针,分别指向数组第一位,同时开始遍历
- 比较两根指针指向的值,如果二者差值小于当前最小值,那么更新最小值
- 移动二者之间较小的那个
- 直到任意一个数组遍历结束
代码实现
public int smallestDifference(int[] arr1, int[] arr2) {
Arrays.sort(arr1);
Arrays.sort(arr2);
int diff = Integer.MAX_VALUE;
for (int i = 0, j = 0; i < arr1.length && j < arr2.length; ) {
if (Math.abs(arr1[i] - arr2[j]) < diff) {
diff = Math.abs(arr1[i] - arr2[j]); // 更新最小值
} else if (arr1[i] < arr2[j]) { // 移动两根指针当中较小的那个
i++;
} else {
j++;
}
}
return diff;
}
分析
时间复杂度O(n logn),空间复杂度O(1)
由于使用了内置的排序方法,所以消耗了O(n logn)的时间复杂度
4.案例: 最短无序连续子数组
给定一个整数数组,找到一个连续子数组。按升序对这个子数组进行排序,会使整个数组呈现升序。返回最短子数组的长度。
输入: array = [1, 2, 4, 7, 10, 11, 7, 12, 6, 7, 16, 18, 19] 输出: [3, 9]
思路分析 1
这题需要一点逆向思维。我们可以添加额外的辅助数组,来降低解题的难度。
先复制一份数组的副本,进行排序,得到升序的数组。然后将升序数组和原数组进行比较,就能知道哪些部分是需要排序的。
代码实现 1
public int findUnsortedSubarray(int[] nums) {
int[] arr = Arrays.copyOf(nums, nums.length); // 复制数组
Arrays.sort(arr); // 排序
int left = 0; // 从左往右,找到第一个需要排序的位置
while (left < nums.length && arr[left] == nums[left])
left++;
int right = nums.length -1; // 从右往左,找到第一个需要排序的位置
while (right >= 0 && arr[right] == nums[right])
right--;
return left <= right ? right - left + 1: 0; // 如果数组已经是升序,返回0;否则返回长度
}
分析
时间复杂度O(n logn),空间复杂度O(n)
由于使用了内置的复制和排序方法,所以消耗了O(n logn)的时间和O(n)的空间
思路分析 2
有了解法1的思考方向,我们可以对解法进一步优化。我们进一步分析原数组与排序后数组的关系。仔细回看原数组与排序后的数组。
以数组[1, 2, 3, 0]为例,我们可以看出正确的顺序是[0, 1, 2, 3],需要排序的子数组范围为0~3之间。此时我们在数组最后添加两个数字[4, 6]作为一个新的输入数组,通过重排0~3之间的子数组,我们依然可以获得一个升序数组。
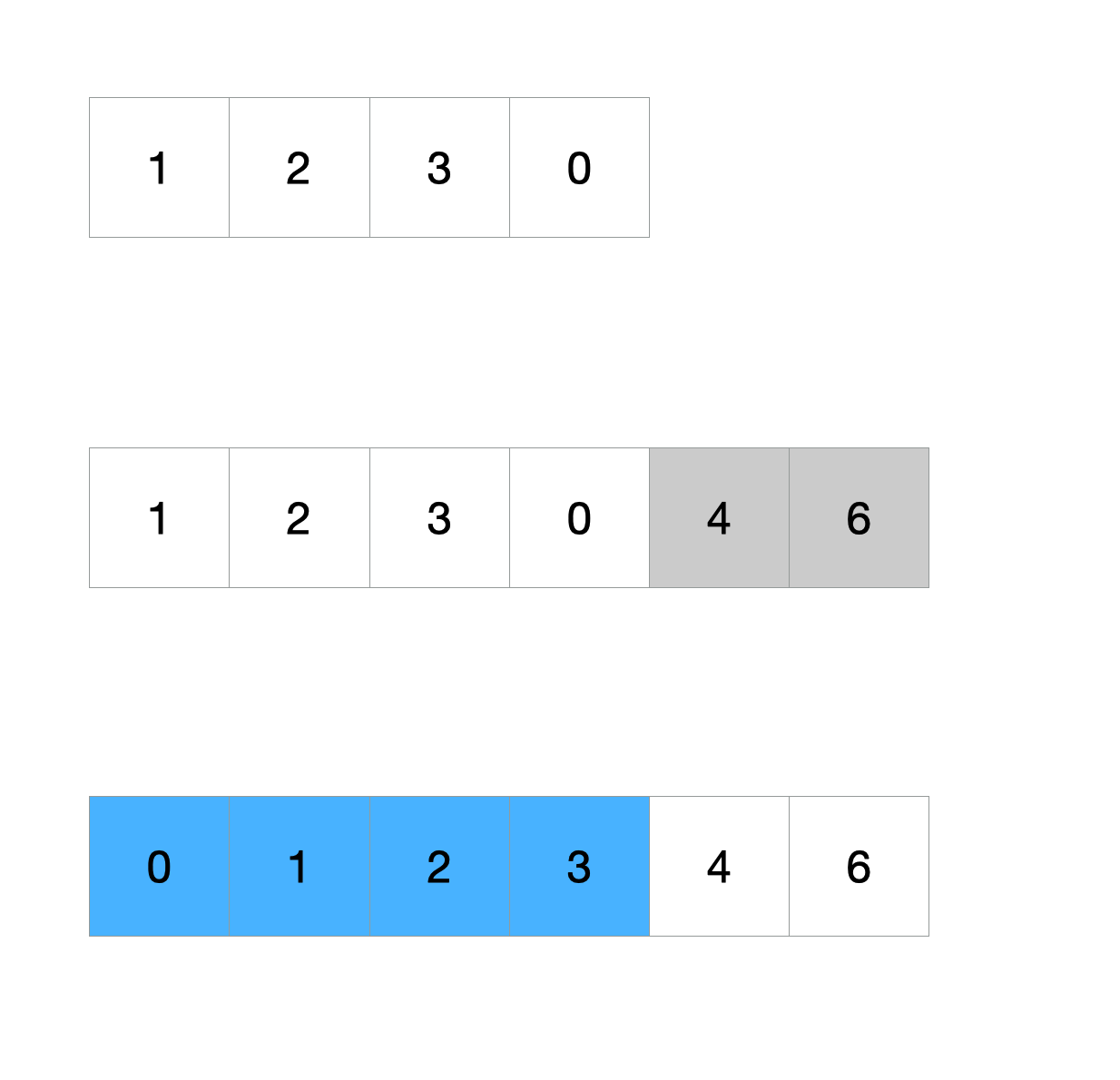
我们将原数组的第三个数字变成5,重复上面的步骤,在数组最后添加两个数字[4, 6]作为一个新的输入数组。此时重排0~3之间的子数组已经不行了。我们需要重排0~4之间的子数组。
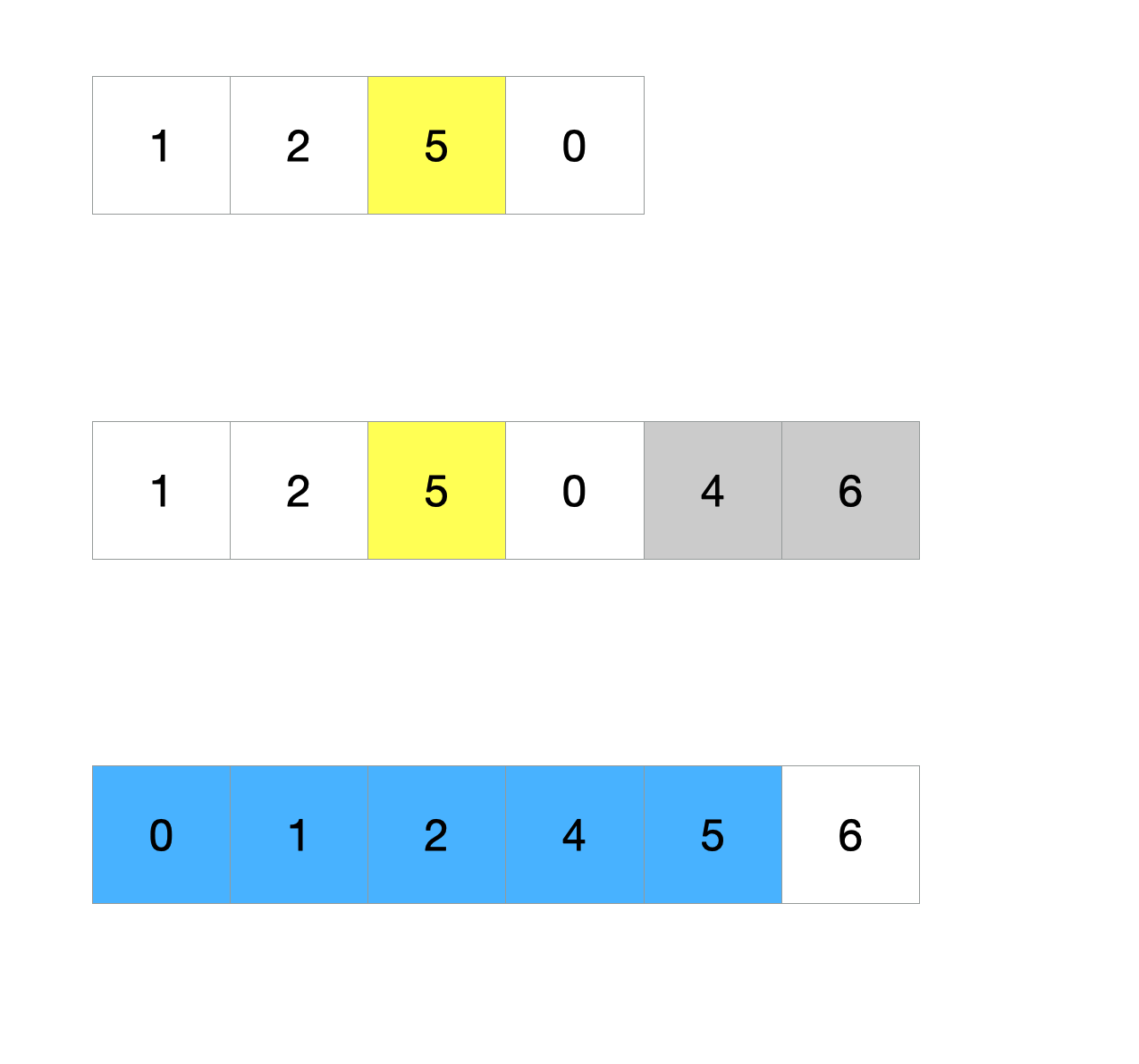
这两个例子说明了两件事:
- 已经排序好的部分也会受到未排序子数组的影响,所以不能用来确定边界
- 需要排序的子数组的边界,是由子数组中的最大值和最小值确定的
有了上面两个推论,算法部分就好办了
- 遍历数组,在未排序的部分中,找到子数组最大值和最小值
- 利用子数组最大值和最小值确定需要排序的子数组的边界
- 根据边界,返回子数组的长度
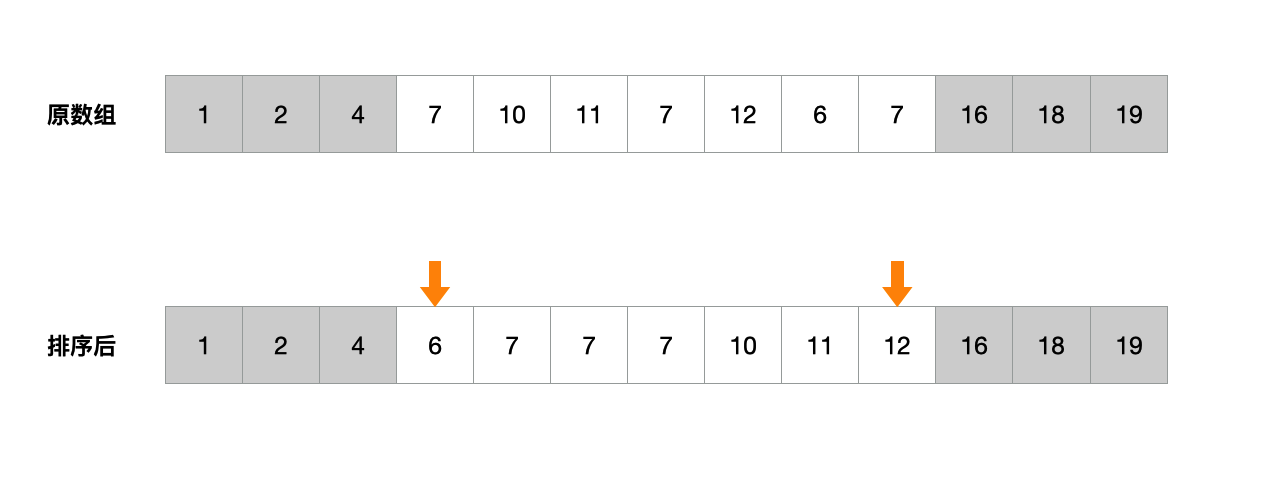
代码实现 2
public int findUnsortedSubarray(int[] nums) {
if (nums == null || nums.length <= 1)
return 0;
int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
for (int i = 0; i < nums.length; i++) // 遍历数组
if (!sorted(nums, i)) { // 找到未排序的部分,确定最大值和最小值
min = Math.min(min, nums[i]);
max = Math.max(max, nums[i]);
}
int left = 0; // 从左往右,找到最小值的位置,即为左边界
while (left < nums.length && nums[left] <= min)
left++;
int right = nums.length - 1; // 从右往左,找到最大值的位置,即为右边界
while (right >= 0 && max <= nums[right])
right--;
// 如果数组已经是升序,返回0;否则返回长度
return left < right ? right - left + 1 : 0;
}
boolean sorted(int[] nums, int i) {
if (i == 0) return nums[i] <= nums[i + 1];
if (i == nums.length - 1) return nums[i - 1] <= nums[i];
return nums[i - 1] <= nums[i] && nums[i] <= nums[i + 1];
}
分析
时间复杂度O(n),空间复杂度O(1)
这种解法只使用了两根指针,最多需要遍历三遍数组,所以时间复杂度O(n),空间复杂度O(1)。本题大部分时间复杂度O(n)的解法都是这种解法的变种。优化之后可以在一次遍历中,同时确定左右边界,但是可读性会差于现在的解法。
总结
本章我们初步认识了数组,体会了数组类算法题的出题方式
习题
- 给出两个非空整数数组,判断第二个数组是否是第一个数组的子序列。 输入: array1 = [5, 1, 22, 25, 6, -1, 8, 10] array2 = [1, 6, -1, 10] 输出: true