Day 27 Dynamic Programming 动态规划 1

在之前的章节里，我们已经学习了基本的数论类问题：排列组合。从本节开始，我们将进一步学习更高难度的数论类问题。这一类题目一般被划分为动态规划类。实际上，动态规划本身并不是一种编程方式或数据结构，而是一种思想。动态规划类的题目多种多样，他们的共同点在于常规解法会造成指数级的时空复杂度消耗。面试时，动态规划问题被认为是所有题目中最高难度的一种。

核心算法——子集和

subset sum问题，一般被称为背包问题。题目形式比较固定，一般会给出一个集合和一个约束条件，要求从集合中取出特定的元素满足条件。比如：

给出N种水果和他们的重量&价格，判断如何放入容量为K的背包使受益最大。
给出一个数组nums和一个target，判断取哪些数字能使总和为target
给出一个数组nums和一个target，判断添加哪些运算符号能使结果为target
……

这类题目是最典型的动态规划问题之一，通通是从集合中选取满足条件的子集。他们的解法是满足固定套路：使用一维或二维数组dp来记录动态规划的状态，再根据递推公式自顶向上推导出满足条件的最终状态。部分题目还可以利用压缩数组的方式来降低空间消耗。

1.案例: 非相邻最大子集和

小偷沿着一条街偷窃，每个房子内有特定金额。相邻的房子防盗系统相互联系，且相邻的两个房子被偷窃时，系统会自动报警。在不被发现的情况下，小偷最多可以得到多少钱。

输入: [75, 105, 120, 75, 90, 135] 输出: 330 // 75 + 120 + 135

思路分析1

本题需要先从描述中抽象出题目：给定一组正整数，计算该数组内非相邻元素的最大和。有了简化后的描述揭示了题目内涵的数学关系和约束条件：

我们要从一组正整数中选取一部分数字，使他们的和最大
被选取的数字不能相邻

我们使用n[i]表示第i个数字，max[i]表示前i个数字中最大的非相邻子集和。

当i = 1，即只有一个正整数时，max[1] = n[1]。当i = 2时，根据约束条件2，我们只能选两个数中最大的，max[2] = max(n[1], n[2]) 当i = 3时，根据约束条件2，我们需要做出选择：

选取n[3]，max[3] = n[3] + max[1]
不选取n[3], max[3] = max[2]

在接下来的每一步，我们都需要做这样的选择。因此我们可以得到递推公式：max[k] = max ( n[k - 1], max[k - 2] + n[k]).

我们将上面的分析转变成代码，需要记住的数组是从0位开始的

代码实现1

public int rob(int[] nums) {
    int len = nums.length;
    if (len == 0)   return 0;
    // 只有一个正整数
    if (len == 1)   return nums[0];

    int[] dp = new int[len];
    // 第一个数字不用选择
    dp[0] = nums[0];
    // 第二个数字选两个数中最大的
    dp[1] = Math.max(nums[0], nums[1]);
    // 从第三步开始，每一步要选择
    for (int i = 2; i < nums.length; i++) {
        // 递推公式：max[k] = max ( n[k - 1], max[k - 2] + n[k])
        dp[i] = Math.max(dp[i - 1], nums[i] + dp[i - 2]);
    }
    // 最后一位就是答案
    return dp[len - 1];
}

思路分析2

解法1需要消耗时间复杂度O(n)，空间复杂度O(n)。这是因为我们使用了一个长度为n的数组dp。再次观察递推公式，我们可以发现因为max[k] = max ( n[k - 1], max[k - 2] + n[k])，第k位的值只依赖于k-1和k-2两位。所以我们可以通过取余来压缩数组

代码实现2

public int rob(int[] nums) {
    int len = nums.length;
    if (len == 0)   return 0;
    if (len == 1)   return nums[0];

    // 将数组长度压缩到2
    int[] dp = new int[2];
    // 初始化过程保持不变
    dp[0] = nums[0];
    dp[1] = Math.max(nums[0], nums[1]);
    for (int i = 2; i < nums.length; i++) {
        // 递推公式：max[k] = max ( n[k - 1], max[k - 2] + n[k])
        // 通过取余来压缩数组
        dp[i % 2] = Math.max(dp[(i - 1) % 2], nums[i] + dp[(i - 2) % 2]);
    }
    // 最后一位同样要取余
    return dp[(len - 1) % 2];
}

分析

时间复杂度O(n)，空间复杂度O(1).

2.案例: 最少硬币交换

给出一组硬币面额以及一个总金额n，计算最少要多少硬币才能达到该金额。如果无法与总金额面额相等，返回-1.

输入: [1, 5, 10], n = 7 输出: 3 // 1 + 1 + 5

思路分析

我们先提取出数学关系：从给定的数组中取出多个数，使总和达到n。我们使用dp[i]表示到达i需要的最少硬币个数。我们先给每一位一个极大值，然后逐步减少，最终收敛到最少硬币个数。假设dp[i] = k, k依赖于k - 1位置。dp[i - c] = k - 1，代表k - 1个硬币能到达金额i - c，c是一枚硬币的面值。假设给定的一组硬币面值为[C1, C2, C3]，我们可以得到递推公式dp[k] = min (dp[i - C1], dp[i - C2], dp[i - C3]) + 1

代码实现

public int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    // 设定最大值
    int MAX = amount + 1;
    // 将dp数组初始化成最大值
    Arrays.fill(dp, MAX);
    // 需要0个硬币到达总金额0
    dp[0] = 0;
    // 动态规划
    for (int i = 1; i <= amount; i++) {
        for (int c: coins) {
            if (i >= c) {
                // dp[k] = min(dp[i - C_n]) + 1
                dp[i] = Math.min(dp[i], dp[i - c] + 1);
            }
        }
    }
    // 如果无法达到，返回-1；否则返回硬币数
    return dp[amount] == MAX ? -1 : dp[amount];
}

分析

时间复杂度O(T * n)，空间复杂度O(T)。T代表amount的值。

3.案例: 硬币交换方案

给出一组硬币面额以及一个总金额n，计算有多少种方案能是硬币总计达到该金额。

输入: [1, 2, 5], N = 5 输出: 4

思路分析

本题的数学关系与上一题相似：从给定的数组中取出多个数，使子集和达到n，计算有多少种取法。

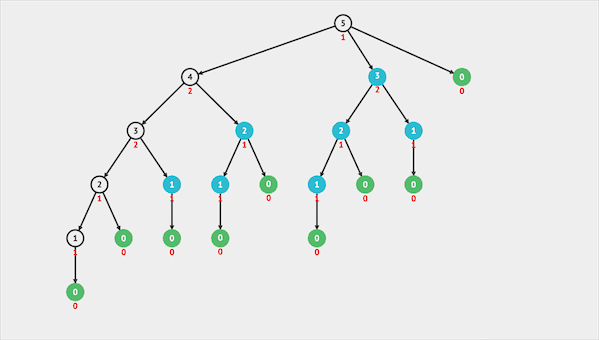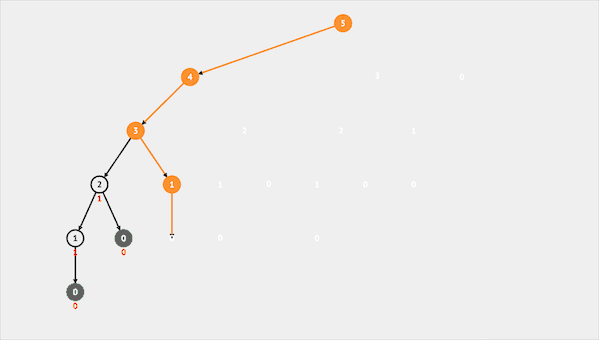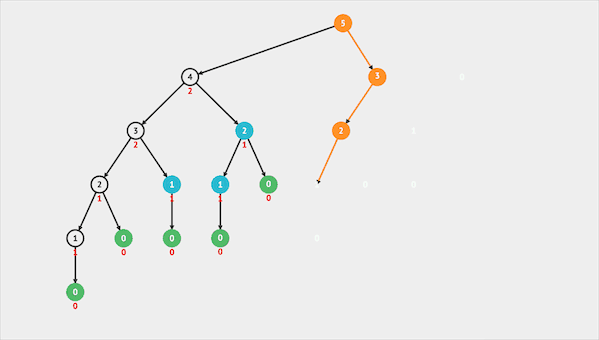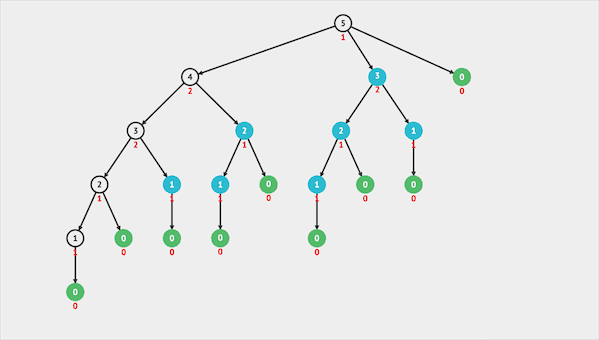
图片由visualgo制作

我们使用dp[i]表示有多少个子集的子集和为n。我们先给每一位初始化为0，每发现一种子集将该值加一。

假设给定的一组硬币面值为[C1, C2, C3]，dp[i - C1] = a, dp[i - C2] = b, dp[i - C3] = c. 最终dp[i] = a + b + c. 我们可以得到递推公式dp[k] = sum (dp[i - C1], dp[i - C2], dp[i - C3]).

代码实现

public int change(int amount, int[] coins) {
    // 将dp数组初始化成0
    int[] dp = new int[amount + 1];
    // 金额0只有唯一方案
    dp[0] = 1;
    for (int c : coins) {
        for (int i = 1; i <= amount; i++) {
            if (i >= c) {
                // 递推公式：dp[k] = sum (dp[i - C_n])
                dp[i] += dp[i - c];
            }
        }
    }
    // 返回方案数
    return dp[amount];
}

分析

时间复杂度O(T * n)，空间复杂度O(T)。T代表amount的值。

4.案例: 划分和相等的子集

给出一个正整数数组, 判断是否可以划分为两个元素和相等的子集。

输入: [1, 2, 3, 4] 输出: True // [1, 4] & [2, 3]

思路分析1

本题符合子集和问题的模式，数学关系比较简单，甚至可以用前一章节排列组合问题的backtracing法来解决。但是backtracing的时空复杂度消耗是指数级的。使用动态规划可以将时空复杂度消耗降到多项式级别。我们的最终目的是判断能否从数组中找出特定子集和的子集，因此我们需要一个二维dp数组来记录状态。

dp[i][s]为true代表我们可以从前i个数字中找到一个总和为s的子集。对于每一个数字（num[i]）我们有两种选择：

不选择当前数字，那么我们得到的总和s会与前i-1个数字的情况一样，即dp[i][s] = dp[i - 1][s]
选择当前数字（并且当前数字不超过s），那么我们需要从前i-1个数字中找到一个子集和为s-num[i]，即dp[i][s] = dp[i - 1][s - num[i]]

以上两种情况任何一种为true，dp[i][s]都为true。因此获得递推公式：dp[i][s] = dp[i - 1][s]

dp[i - 1][s - num[i]]

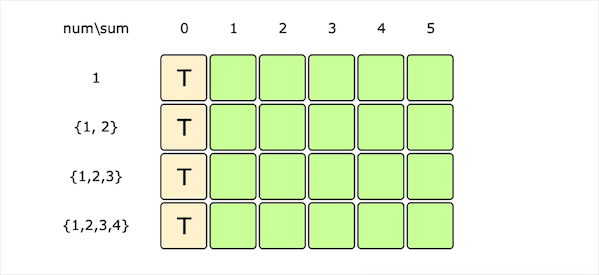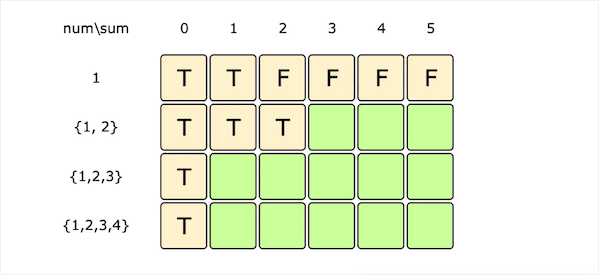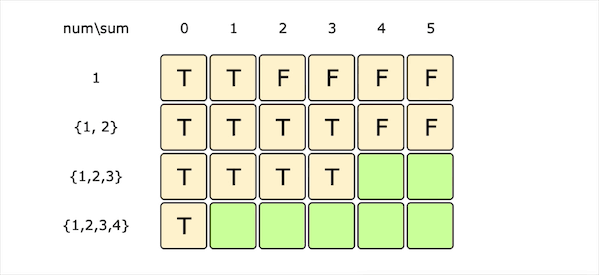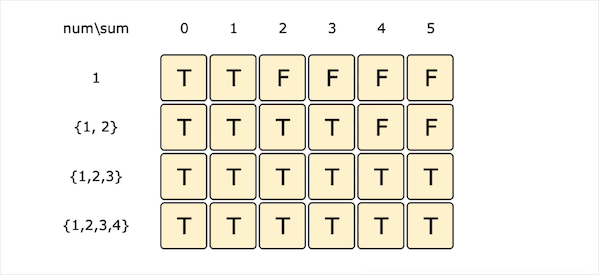
图片由visualgo制作

代码实现1

public boolean canPartition(int[] nums) {
    // 计算数组总和
    int sum = 0;
    for (int n : nums)
        sum += n;
    // 如果总和不能被2整除，说明无法划分
    if (sum % 2 == 1) return false;

    sum /= 2;
    int len = nums.length;
    // 建立一个二维数组记录状态
    // dp[i][s]代表能否从前i个数字中找到一个总和为s的子集
    boolean[][] dp = new boolean[len][sum + 1];
    // 总和为0的子集一定存在
    for (int i = 0; i < len; i++)
        dp[i][0] = true;
    // 动态规划
    for (int i = 1; i < len; i++) {
        for (int j = 0; j <= sum; j++) {
            // 不选择当前数字，当前总和等于前i-1个数子集的总和
            dp[i][j] |= dp[i - 1][j];
            if (j >= nums[i])
                // 选择当前数字，需要从前i-1个数字中找到一个子集和为s-num[i]
                dp[i][j] |= dp[i - 1][j - nums[i]];
        }
    }
    // 返回最终结果
    return dp[len - 1][sum];
}

思路分析2

解法1需要消耗时间复杂度O(T * n)，空间复杂度O(T * n)，T代表sum的值。再次观察递推公式，我们可以发现dp[i]行的值只依赖与dp[i - 1]行的值。所以我们可以通过压缩数组来降低复杂度。

代码实现2

public boolean canPartition(int[] nums) {
    // 计算数组总和
    int sum = 0;
    for (int n : nums)
        sum += n;
    // 如果总和不能被2整除，说明无法划分
    if (sum % 2 == 1) return false;

    sum /= 2;
    int len = nums.length;
    // 建立一个二维数组记录状态，并压缩到两行
    boolean[][] dp = new boolean[2][sum + 1];
    // 总和为0的子集一定存在
    dp[0][0] = true;
    dp[1][0] = true;
    // 动态规划
    for (int i = 1; i < len; i++) {
        for (int j = 0; j <= sum; j++) {
            // 不选择当前数字，当前总和等于前i-1个数子集的总和
            // 对2取余，压缩状态
            dp[i % 2][j] |= dp[(i - 1) % 2][j];
            if (j >= nums[i]) {
                // 选择当前数字，需要从前i-1个数字中找到一个子集和为s-num[i]
                // 对2取余，压缩状态
                dp[i % 2][j] |= dp[(i - 1) % 2][j - nums[i]];
            }
        }
    }
    // 返回最终结果
    return dp[(len - 1) % 2][sum];
}

分析

时间复杂度O(T * n)，空间复杂度O(T)，T代表sum的值

总结

本章我们学习了子集和问题（也被成为背包问题）。不同于之前的排列组合，我们使用了动态规划的方法将时空复杂度从指数级降低到了多项式级别。动态规划类问题的核心在于从题目中提取出数学关系和推到递推公式。这类题目虽然套路固定，但是递推公式各不相同。需要读者多加练习，勤于思考。

习题

给定一个非负整数的数组和一个目标S。用+和-两种运算，计算有多少种方法使得这些整数的和正好等于S。
给定一个整数数组nums和一个正整数k，判断能否把这个数组分成k个非空的子集，子集和全部都相等。