Day 13 - Queue 队列
上一节我们学习了经典的Stack栈结构和常见考点单调栈,本节课我们来学习Queue队列。
相比于Stack,Queue其实只是逻辑上存在的数据结构,单纯地实现Queue意义不大。(大家有时间可以自己试着实现以下,最终应该会写成LinkedList的等价形式。)Queue的行为其实完全可以用LinkedList来代替,Java中也是这么做的,使用LinkedList实现了Queue的接口。
Queue queue = new LinkedList();
那么Queue类的问题到底是在考察什么呢?答案是数据顺序。更进一步说,是后进先出LIFO和先进先出FIFO两种顺序的正确选择。
基础知识——队列
Queue 队列也可以看做是一种特殊的线性表,元素只能从队列尾部插入,从队列头部访问、删除,按照先进先出(FIFO, First In First Out)的顺序运作。所以使用LinkedList实现队列比使用ArrayList实现更加高效。在Java中,没有提供默认的Queue的实现,仅提供了Queue的接口。常用的两种Queue的实现类为ArrayDeque和LinkedList。ArrayDeque使用了动态循环数组,并且实现了Deque双端队列的API,在多数场景下更加高效。
Queue的主要API有三个:offer插入, poll删除, peek访问。
- offer只能将元素插入队列尾部。
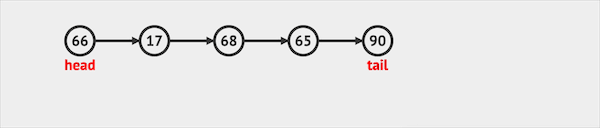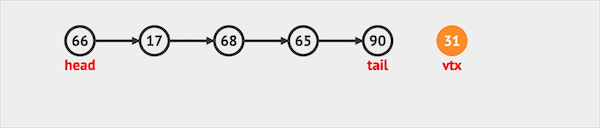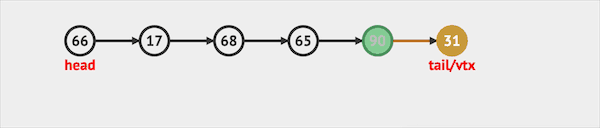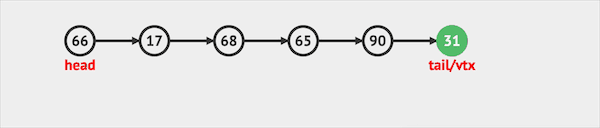
图片由visualgo制作
- poll只能将元素从队列头部移除。
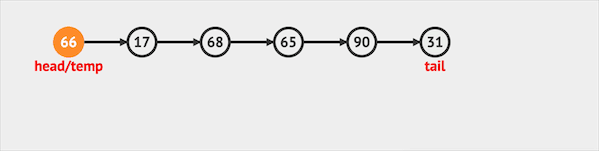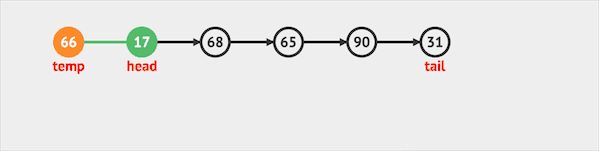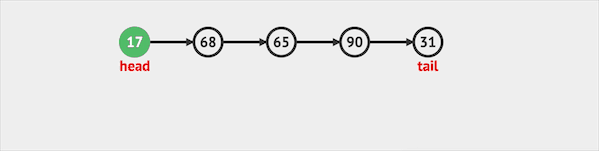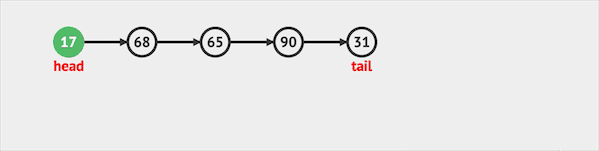
图片由visualgo制作
- peek访问返回队列头部元素,但是不删除。
1.案例: 用栈实现队列
使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作。
思路分析
题目的本意是要求我们用LIFO序列模拟FIFO序列,并且在题干中给出了提示:用两个Stack模拟一个Queue。Queue的操作只有三个:加入、移除、访问。
我们利用两个Stack:一个负责加入元素,一个负责移除元素。每次push时,直接向in中加入元素。pop或者peek时,先查看out中是否有缓存好的元素,如果已经存在元素,那么直接返回out的栈顶元素。如果没有,那么将in中的元素弹出加入out,直到in为空为止。比如数字按1,2,3的顺序加入in;当in弹出元素加入out时,顺序会变成3,2,1;当out再弹出元素时,顺序会回复成1,2,3,满足FIFO的顺序。
代码实现
class MyQueue {
private Stack<Integer> in, out;
public MyQueue() {
in = new Stack<>(); // in负责加入元素
out = new Stack<>(); // out负责弹出元素
}
public void push(int x) {
in.push(x); // push时,直接向in中加入元素
}
public int pop() {
peek(); // 确保out中存在缓存好的元素
return out.pop();
}
public int peek() {
if (out.isEmpty()) // 先查看out中是否有缓存好的元素,
while (!in.isEmpty()) // 将in中的元素弹出加入out,直到in为空为止
out.push(in.pop());
return out.peek(); // 返回out的栈顶元素
}
public boolean empty() {
return in.isEmpty() && out.isEmpty();
}
}
2.案例: 用队列实现栈
使用两个队列实现后入先出栈。栈应当支持一般栈支持的所有操作。
思路分析
本题与上一题相反,要求我们用FIFO序列模拟LIFO序列,并且提示:用两个Queue模拟一个Stack。Stack的操作同样只有三个:加入、移除、访问。
我们需要利用两个Queue。每次加入的时候,把元素插入到queue的头部,那么也就形成了类似栈的出入顺序:
- 创建一个临时队列temp,将原来queue里的元素移入temp(queue被清空)
- 将新的元素加入queue(此时queue中只有这一个元素,并且排在第一位)
- 等新元素进入queue之后,再将之前temp中的元素加入queue,排在新元素后面
移除元素时,直接从queue的头部移除。
代码实现
class MyStack {
Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
// 创建一个临时队列temp,将原来queue里的元素移入temp(queue被清空)
Queue<Integer> temp = queue;
queue = new LinkedList<>();
// 将新的元素加入queue
queue.offer(x);
// 等新元素进入queue之后,再将之前temp中的元素加入queue,排在新元素后面
while (!temp.isEmpty()) {
queue.offer(temp.poll());
}
}
public int pop() {
// 直接从queue的头部移除
return queue.poll();
}
public int top() {
// 直接从queue的头部获取
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
核心算法——双端队列
Deque 双端队列(全名double-ended queue)是一种同时具有Queue和Stack性质的数据类型。双端队列中的元素可以从两端弹出,插入和删除。Java中提供了LinkedList和ArrayDeque两种实现,推荐使用ArrayDeque。Deque是Queue类考题中最常出现的解题技巧。
Java中将一端定义为First,一端定义为Last。Deque提供addFirst, addLast, removeFirst, removeLast, getFirst, getLast 六种基础API。(注意不要Last-In-First-Out序列,First-In-First-Out序列的概念混淆)。基于基础API,Deque同时支持offer/poll/push/pop/peek 这两套操作。
3.案例: 数据流滑动窗口平均值
给出一串整数流和窗口大小,计算滑动窗口中所有整数的平均值。
思路分析
题目要求我们对数据流上一个固定大小的区间进行计算,这种计算模型叫做滑动窗口。滑动窗口是经典考察模板之一,我们在之后会详细论述。对于这题而言,我们需要一个数据结构来保存这段区间,并且不断关系区间里的数据:按照FIFO的顺序,弹出旧数据,加入新数据。同时由于本题给定了固定的窗口大小,所以最好的方法是使用循环数组来实现Queue。在Java中ArrayDeque正是用循环数组实现的。
我们使用一个额外的sum字段记录当前区间内的数字和。每当新的数字加入,除了从queue中弹出旧数据,加入新数据,我们还需要在sum上减去旧数据,加入新数据。最后用sum除以queue的大小,得到当前的平均值。
代码实现
class MovingAverage {
Deque<Integer> queue;
int size;
double sum;
public MovingAverage(int size) {
queue = new ArrayDeque<>(); // 初始化一个队列
this.size = size;
sum = 0;
}
public double next(int val) {
queue.offer(val); // 加入新数据
sum += val; // 加入新数据
if (queue.size() > size) { // 如果当前队列的大小,超出窗口大小
sum -= queue.poll(); // 弹出旧数据,并从sum减去旧数据
}
return sum / queue.size(); // 用sum除以queue的大小,得到当前的平均值
}
}
分析
时间复杂度O(1),空间复杂度O(n)
4.案例: 简化路径
给定一个文件的绝对路径(Unix-style),请进行路径简化。Unix中, . 表示当前目录, .. 表示父目录。结果必须以 / 开头,并且两个目录名之间有且只有一个 /。最后一个目录名(如果存在)后不能出现 / 。你需要保证结果是正确表示路径的最短的字符串。
输入: path = “/foo/../test/../test/../foo//bar/./baz” 输出: “/foo/bar/baz”
思路分析
对于这道题,一个直观的想法是利用栈处理。首先将原字符串以’/’分隔, 然后遍历:
- 遇到正常的目录名, 那么执行压栈
- 遇到 ‘.’ 或空名称 (对应 “//”) ,那么忽略
- 遇到 “..” ,则从栈顶弹出一个元素
- 如果栈为空,则忽略不弹栈 (对应 “/../”)
- 最后将栈中的元素以 ‘/’ 连接得到结果
但是在最后一步连接栈中元素时,会出现一个问题:从栈中弹出的元素时反序。直接使用stack的话,我们需要先缓存弹出的序列,然后翻转,最后连接。
对应的解决方案有三种:
- 使用list,并且每次只在尾端操作,来代替stack的功能
- 利用stack的父类vector的API,通过迭代器在stack上做正序访问
- 使用deque代替stack
这三种方法对应着三种数据结构,但是在逻辑层面是一样的:我们需要一个数据结构,能够在处理原字符串时遵循LIFO顺序,在最后拼接字符串时遵循FIFO顺序。所以选择方法3是最正确的方式(方法1和2同样可行,但是可读性不如方法3)。
代码实现
public String simplifyPath(String path) {
String[] dirs = path.split("/"); // 将原字符串以'/'分隔
Deque<String> deque = new ArrayDeque<>(); // 使用deque代替stack
for (String dir: dirs) {
switch (dir) {
// 遇到'.'或空名称,忽略
case ".":
case "":
continue;
// 遇到 ".."
case "..":
if (!deque.isEmpty()) {
deque.removeLast(); // 从栈顶弹出一个元素
}
// 如果栈为空,则忽略
continue;
default:
deque.addLast(dir); // 遇到正常的目录名, 压栈
}
}
StringBuilder builder = new StringBuilder();
while (!deque.isEmpty())
builder.append("/").append(deque.removeFirst()); // 拼接字符串时遵循FIFO顺序
// 对于空路径返回/,其余返回拼接好的路径
return builder.length() == 0 ? "/" : builder.toString();
}
分析
时间复杂度O(n),空间复杂度O(n)
总结
这节课我们学习了Queue队列和Deque双端队列在面试题中的应用。Queue类题目在面试中出现频率并不高,大多数时候是作为Stack的补充考题出现。