Day 19 - Graph 图 3
上一节我们重温了DFS和BFS算法,并且研究了他们在图搜索类面试题中的应用。本章我们来看Topological Sort 拓扑排序。
拓扑排序通常用于在一大堆依赖关系中寻找线性顺序。在拓扑排序中,如果X依赖于Y,那么排序的结果会使Y出现在X之前。拓扑排序的原理非常直观,并且在生活中非常常见,比如选课时要先修课程A然后才能选课程B,工程上jar包C依赖于jar包D,等等。
核心算法——Topological Sort
一个有向图的拓扑序是它包含的所有节点的一种线性顺序。对于每条从U到V的有向边(U, V),在拓扑序中U会排在V之前。
我们先讲解几个基础概念:
- 入度 & 出度:入度和出度表示了节点与边的关系。假设有向图只包含从u到v的有向边u->v,我们称u的出边条数为1,即出度为1;v的入边条数为1,即入度为1。
- Source 源点 & Sink 汇点:源点 & 汇点借用了水流的概念。Source 源点代表只向外流出的点,只有出度,没有入度。Sink 汇点代表只向内流入的点,只有入度,没有出度。
- 拓扑排序的顺序从一个source出发,终点是一个sink。
- 只有不包含环路的图才能进行拓扑排序。
拓扑排序的逻辑满足BFS的遍历顺序。我们从所有的source出发,向外拓展。每一步将source保存进一个列表,然后删除source。删除source后会产生新的source,我们需要重复上一步。直到访问完所有节点。
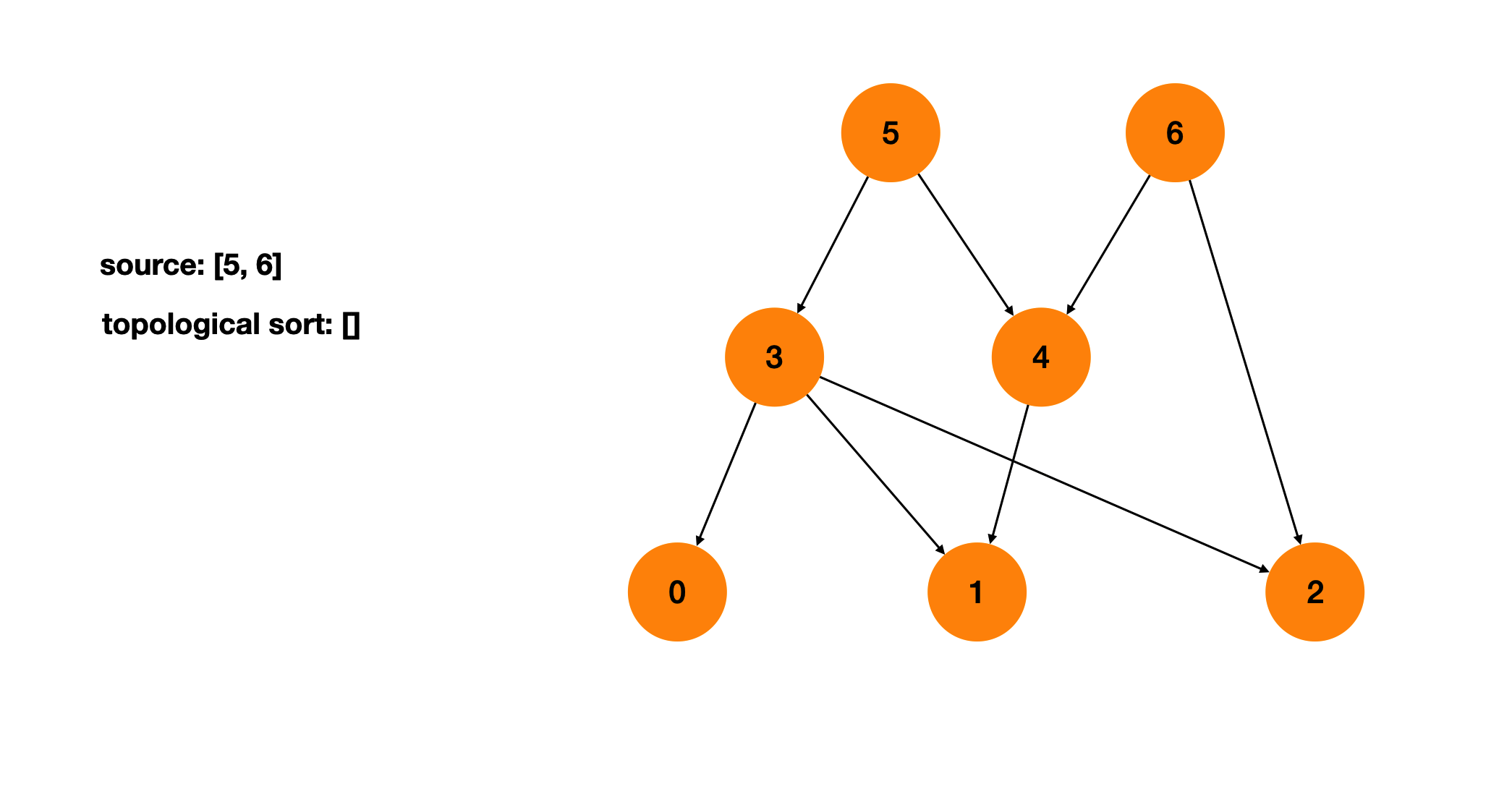
将所有的source添加到列表
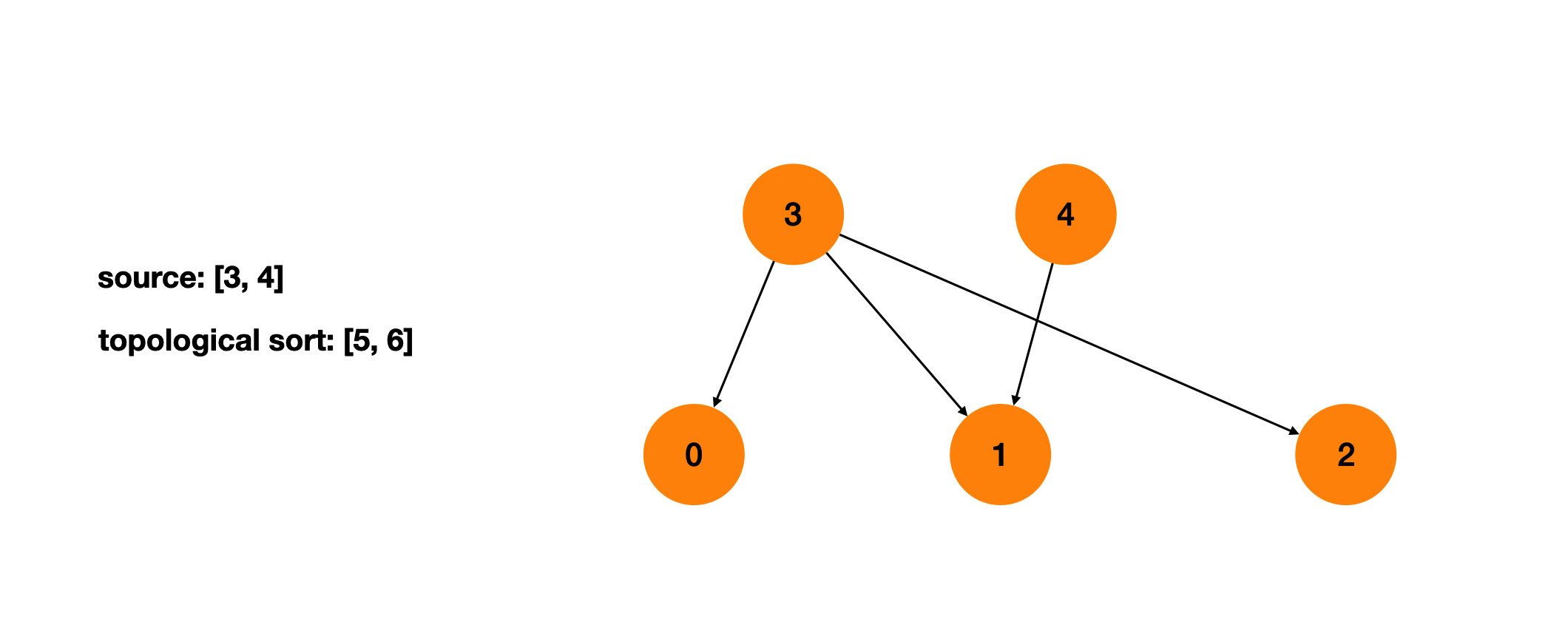
删除source后会产生新的source
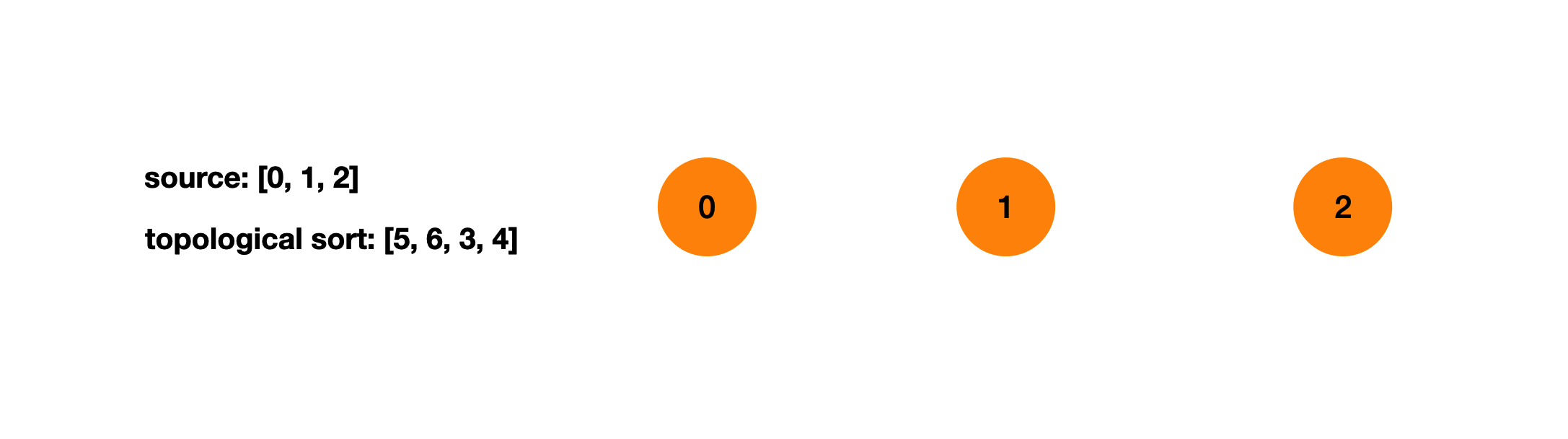
重复上一步,直到访问完所有节点
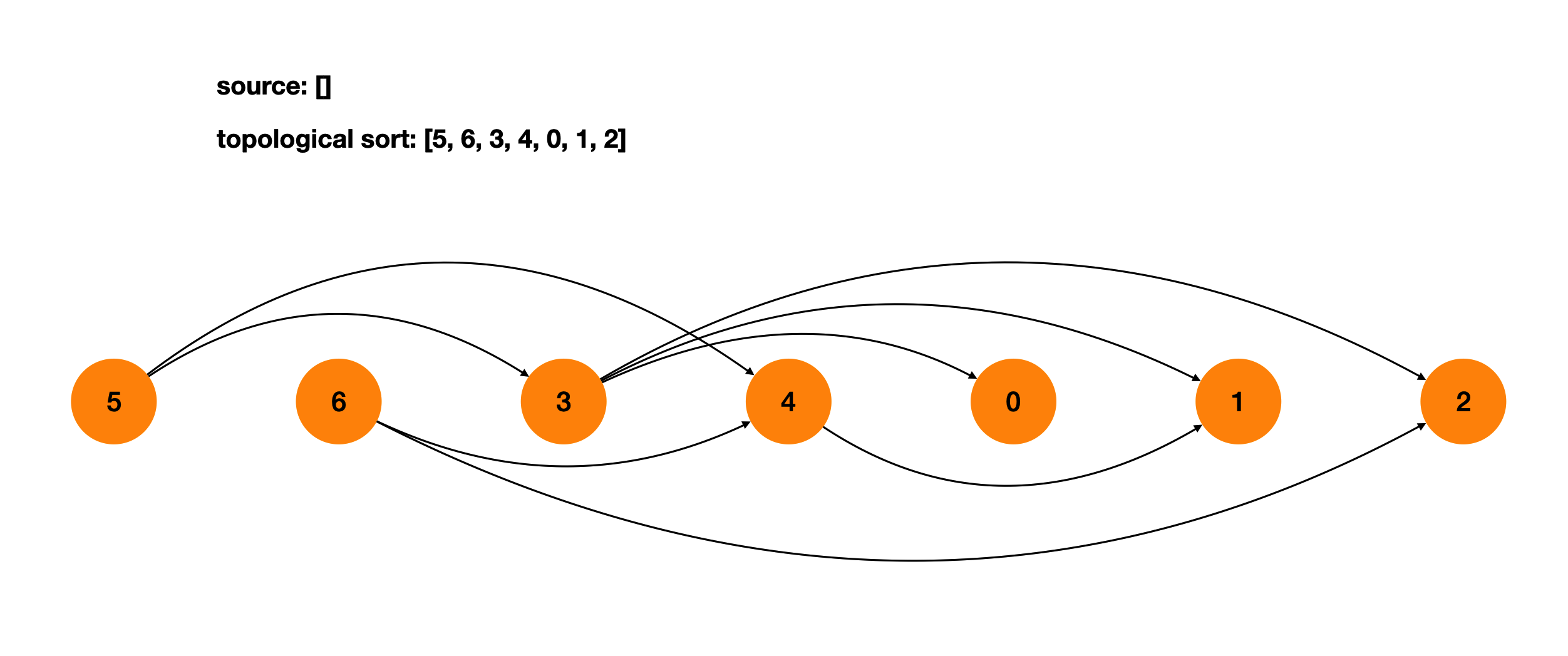
将所有的节点按照拓扑排序的顺序排在一条线上,每条边都是从左指向右的。
1.案例: 课程规划顺序
现在你总共有n门课需要选,记为 0 到 n - 1. 一些课程在修之前需要先修另外的一些课程,比如要学习课程0你需要先学习课程1,表示为[0,1]。给定n门课以及他们的先决条件,返回一种有效的选课顺序。
输入: n=4, prerequisites=[3, 2], [3, 0], [2, 0], [2, 1] 输出: 以下两种都是有效拓扑排序,返回任意一种
- 3, 2, 0, 1
- 3, 2, 1, 0
思路分析
我们先根据题目给出的prerequisites画出一张图
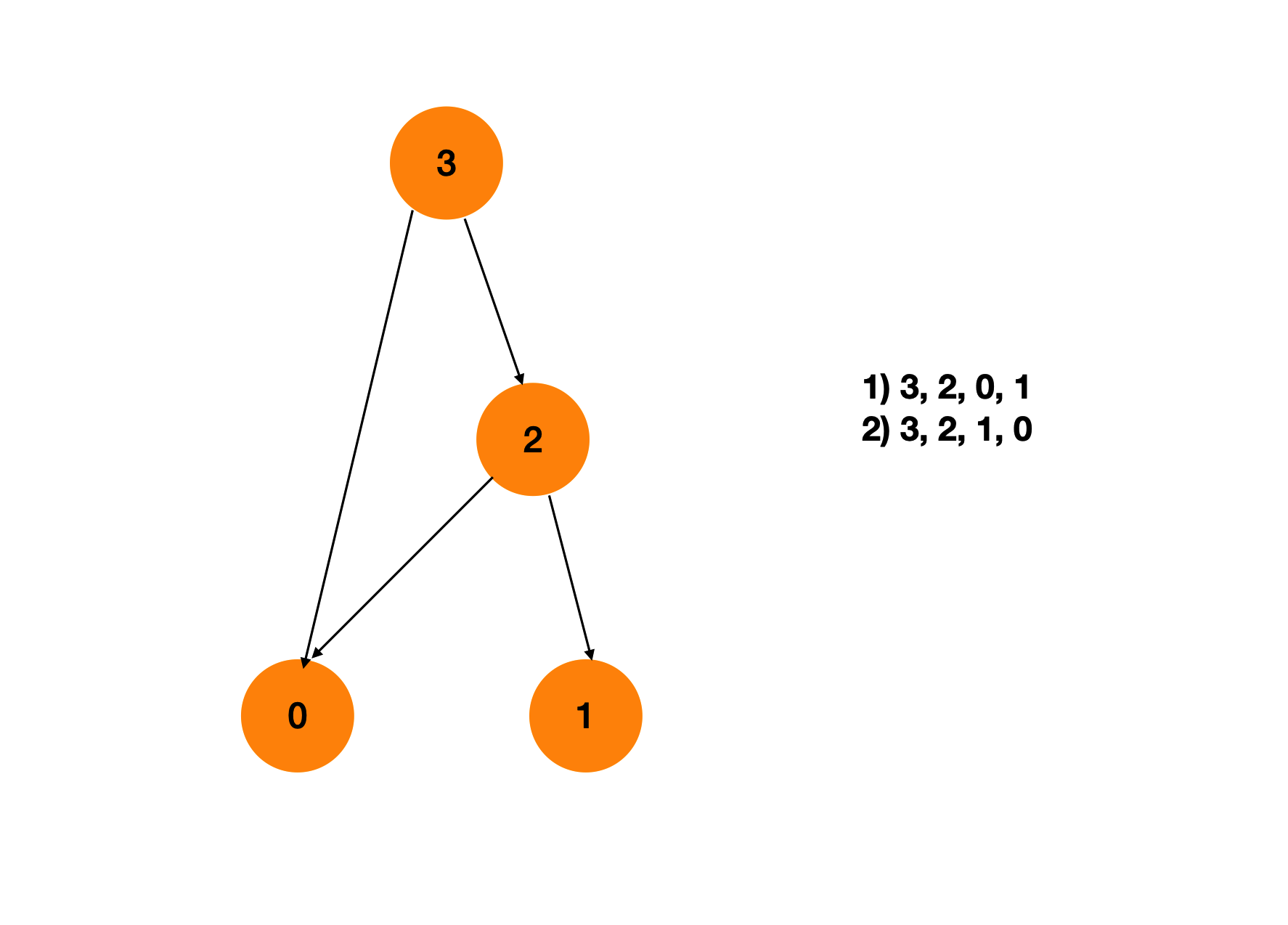
根据两门课之间的约束关系,我们可以将课抽象为节点,将约束抽象为一条有向边。利用拓扑排序解决,一个有效的选课序列就是一个拓扑序。
- 建图并记录所有节点的入度
- 将所有入度为0的节点加入队列
- 从队列中取出一个元素curt
- 访问curt所有的邻接点next,将next的入度减1,当减到0后,将next加入队列
- 重复步骤3、4,直到队列为空
- 如果拓扑序列个数等于节点数,代表存在拓扑序
代码实现
public int[] findOrder(int numCourses, int[][] prerequisites) {
// 建图并记录所有节点的入度
HashMap<Integer, List<Integer>> graph = new HashMap<>();
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int to = edge[0];
int from = edge[1];
graph.putIfAbsent(from, new ArrayList<>());
// 建图,将邻接点加入邻接表
graph.get(from).add(to);
// 记录入度
indegree[to]++;
}
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
// 将所有入度为0的节点加入队列
if (indegree[i] == 0) {
queue.offer(i);
}
}
int[] ans = new int[numCourses];
int i = 0;
while (!queue.isEmpty()) {
// 从队列中取出一个元素curt
int curt = queue.poll();
ans[i++] = curt;
// 访问curt所有的邻接点next
List<Integer> neighbors = graph.getOrDefault(curt, new ArrayList<>());
for (int next : neighbors) {
// 将next的入度减1
indegree[next]--;
// 入度为0,将next加入队列
if (indegree[next] == 0) {
queue.offer(next);
}
}
}
// 如果拓扑序列个数等于节点数,代表存在拓扑序
return i == numCourses ? ans : new int[0];
}
分析
时间复杂度O(V + E),空间复杂度O(V + E)。V代表图的节点数,即课程数。E代表图的边数,即约束条件prerequisite的数量。
2.案例: 外星人词典
有一种使用拉丁字母的外来语言,但是无法得知字母之间的顺序。我们会从词典中收到一个非空的单词列表,并按照新语言的字典顺序排序。找出这种语言的字母顺序。
- 假设所有的字母都是小写。
- 如果a是b的前缀且b出现在a之前,那么这个顺序是无效的。
- 对于无效顺序,则返回空字符串。
- 如果存在多个有效的字母顺序,返回字典序最小的。
输入: [“ywx”, “wz”, “xww”, “xz”, “zyy”, “zwz”] 输出: ywxz
思路分析
一直给定的单词列表是按照字典序排列的,所以我们可以通过比较相邻的两个单词来确定字母之间的顺序。每次取出相邻的两个单词,找到它们之间第一个不同的字母,从中提取出顺序。比如”xww”和”xz”,第2位开始不同,说明w排在z之前。
我们可以将所有的字母看做不同的节点,将整个单词表看做一张图。我们要对这张图做拓扑排序来确定这种语言的字母顺序。
需要注意的是题目中存在一条潜在规则:如果a是b的前缀且b出现在a之前,那么这个顺序是无效的。 比如[“abc”, “ab”],“ab”是“abc”的前缀,但“abc”出现在“ab”之前。这其实违反了一条潜在规则,就是我们认为空字符应该是字符顺序的最前一位。根据我实际尝试,这条规则并不是在所有OJ中都存在。如果在面试中遇上本题,需要和面试官反复确认。
代码实现
public String alienOrder(String[] words) {
// 初始化两张Map,分别作为邻接表和入度表
HashMap<Character, Integer> indegree = new HashMap<>();
HashMap<Character, List<Character>> graph = new HashMap<>();
for (String s : words) {
for (char c : s.toCharArray()) {
// 每个节点的入度初始化为0
indegree.putIfAbsent(c, 0);
// 初始化每个节点的邻接表
graph.putIfAbsent(c, new ArrayList<>());
}
}
// 建图
for (int i = 0; i < words.length - 1; i++) {
String s1 = words[i], s2 = words[i + 1]; // 取得相邻的两个单词
// 如果a是b的前缀且b出现在a之前
if (s1.length() > s2.length() && s1.startsWith(s2))
return ""; // 顺序无效,返回空
for (int j = 0; j < Math.min(s1.length(), s2.length()); j++) {
char c1 = s1.charAt(j), c2 = s2.charAt(j);
// 找到第一位不同的字符
if (c1 != c2) {
// 添加边
graph.get(c1).add(c2);
// 更新入度
indegree.put(c2, indegree.get(c2) + 1);
break;
}
}
}
// 将所有入度为0的节点加入Queue
Queue<Character> queue = new LinkedList<>();
for (char c : indegree.keySet()) {
if (indegree.get(c) == 0) {
queue.offer(c);
}
}
StringBuilder builder = new StringBuilder();
// 拓扑排序
while(!queue.isEmpty()) {
// 从队列中取出一个元素curt
char curt = queue.poll();
// 拼接到结果最末
builder.append(curt);
// 访问curt所有的邻接点
List<Character> neighbors = graph.get(curt);
for (char c : neighbors) {
// 入度减1
indegree.put(c, indegree.get(c) - 1);
// 入度为0,加入队列
if (indegree.get(c) == 0) {
queue.offer(c);
}
}
}
return builder.length() == indegree.size() ? builder.toString() : "";
}
分析
时间复杂度O(V + E),空间复杂度O(V + E)。V代表图的节点数,即字符数。E代表图的边数,即约束条件数(单词列表的长度)。
3.案例: 序列重构
给定一个org序列和一组seqs序列,判断是否能从seqs重构得出唯一的org序列。
输入: originalSeq: [3, 1, 4, 2, 5], seqs: [[3, 1, 5], [1, 4, 2, 5]] 输出: true 输入: originalSeq: [1, 2, 3, 4], seqs: [[1, 2], [2, 3], [2, 4]] 输出: false
思路分析
拓扑排序的思路出发,对于本题我们需要解决两个问题:
- 能否从seqs构造出org
- seqs是否可能构造出多种序列
比如[[1, 2], [2, 3], [2, 4]],既可以构造出[1, 2, 3, 4],又可以构造出[1, 2, 4, 3]。
与前两题相比,本题的重点在于:
- 需要保证构造出来的序列,每一位与org相对应
- 需要保证构造序列时,每一步只有唯一选择
从算法实现的角度看,只要保证queue里最多同时只有一个元素即可
代码实现
public boolean sequenceReconstruction(int[] org, List<List<Integer>> seqs) {
// 初始化两张Map,分别作为邻接表和入度表
HashMap<Integer, List<Integer>> graph = new HashMap<>();
HashMap<Integer, Integer> indegree = new HashMap<>();
for (List<Integer> seq : seqs) {
for (int n : seq) {
// 初始化每个节点的邻接表
graph.putIfAbsent(n, new ArrayList<>());
// 每个节点的入度初始化为0
indegree.putIfAbsent(n, 0);
}
}
// 得到的节点少于org序列包含的节点,一定无法构造成功
if (indegree.size() != org.length) {
return false;
}
// 建图
for (List<Integer> seq : seqs) {
for (int i = 0; i < seq.size() - 1; i++) {
int from = seq.get(i), to = seq.get(i + 1);
graph.get(from).add(to);
indegree.put(to, indegree.get(to) + 1);
}
}
// 将所有入度为0的节点加入Queue
Queue<Integer> queue = new LinkedList<>();
for (int n : indegree.keySet()) {
if (indegree.get(n) == 0) {
queue.offer(n);
}
}
// 指向org的第一位字符
int pos = 0;
// 拓扑排序
while (!queue.isEmpty()) {
// 保证queue里最多同时只有一个元素
if (queue.size() > 1) {
return false;
}
// 从队列中取出一个元素curt
int curt = queue.poll();
// 与org比较,保证构造出来的序列每一位与org相对应
if (curt != org[pos++]) {
return false;
}
// 访问curt所有的邻接点
List<Integer> neighbors = graph.get(curt);
for (int next : neighbors) {
// 入度减1
indegree.put(next, indegree.get(next) - 1);
// 入度为0,加入队列
if (indegree.get(next) == 0) {
queue.offer(next);
}
}
}
// 直到最后一个字符都匹配一致
return pos == org.length;
}
分析
时间复杂度O(V + E),空间复杂度O(V + E)。V代表图的节点数,即字符数。E代表图的边数,即seqs的长度。
4.案例: 最小高度树
给出一个k叉树性质的无向图,可以选择任何一个节点作为根。这个图就变成了一个有根树。在所有可能的有根树中,有最小高度的树叫做最小高度树(MHT, minimum height tree)。给定这样的图,找出所有的MHT,返回根标记的数组。
输入: n: 5, edges: [[0, 1], [1, 2], [1, 3], [2, 4]] 输出: [1, 2]
思路分析
先根据题意画出这棵树
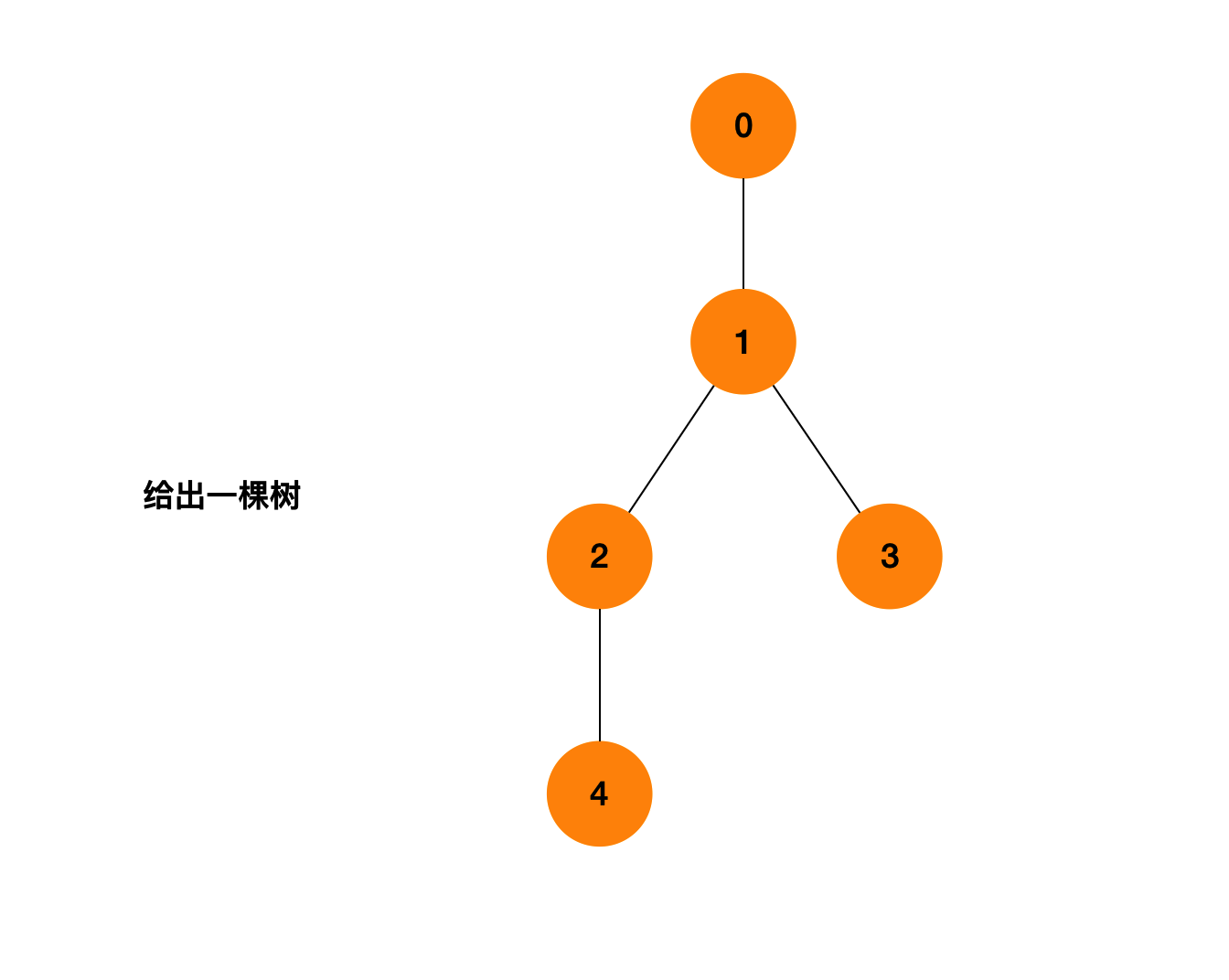
分别尝试用不同的节点作为根节点,并统计高度
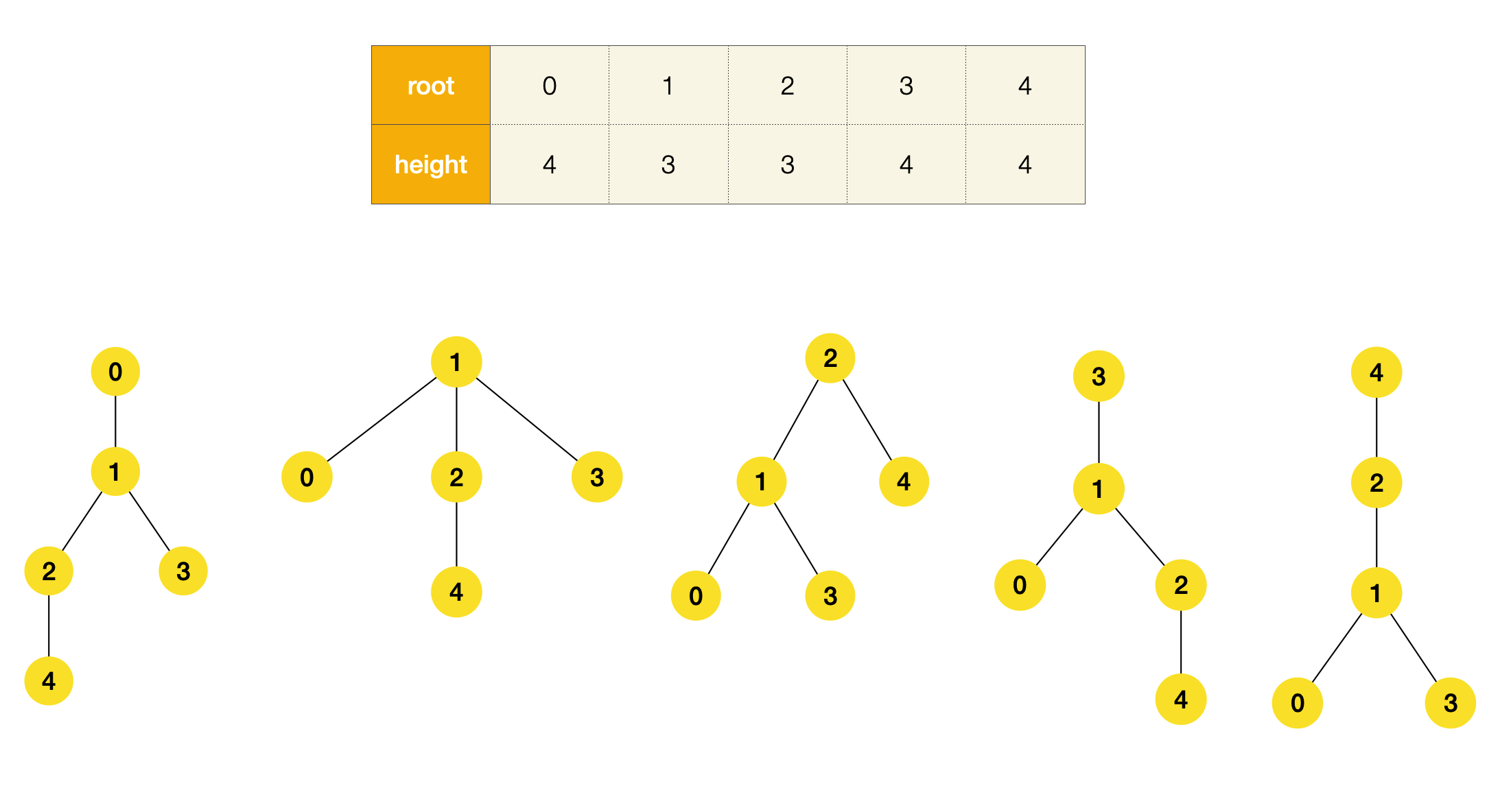
从画图的过程中,我们可以直观地了解到:节点数大于2时,叶子节点不能作为MHT的根节点,因为叶子节点的邻居节点一定能有更小的高度(比如上图中叶子节点[0, 3, 4])。
本题的思路相当于拓扑排序和按层BFS的混合,每次将叶子节点加入queue,然后将叶子节点从原图删去。删去后形成新的图,再取出新的叶子节点加入queue,重复上一步。直到最后一组节点,就是我们要的答案。
- 创建图,统计每个节点的入度
- 把所有入度为1的节点放入queue(叶子节点)
- 把每个叶子节点的邻居节点的入度减1
- 当节点入度为1时,放入queue(新的叶子节点)
- 最后的一组queue就是最后的根节点,也就是答案
代码实现
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
// 只有一个节点时,该节点就是根节点
if (n == 1) {
return Arrays.asList(0);
}
// 初始化两张Map,分别作为邻接表和入度表
HashMap<Integer, List<Integer>> graph = new HashMap<>();
HashMap<Integer, Integer> indegree = new HashMap<>();
for (int i = 0; i < n; i++) {
// 初始化每个节点的邻接表
graph.put(i, new ArrayList<>());
// 每个节点的入度初始化为0
indegree.put(i, 0);
}
for (int[] edge: edges) {
int from = edge[0], to = edge[1];
// 树是无向图,所以每条边需要两个方向
graph.get(from).add(to);
graph.get(to).add(from);
// 同上,入度需要两个方向更新
indegree.put(to, indegree.get(to) + 1);
indegree.put(from, indegree.get(from) + 1);
}
// 把所有入度为1的节点放入queue(叶子节点)
LinkedList<Integer> queue = new LinkedList<>();
for (int node : indegree.keySet()) {
if (indegree.get(node) == 1) {
queue.offer(node);
}
}
// 拓扑排序
while (!queue.isEmpty()) {
int size = queue.size();
// 更新剩下未访问的节点数
n -= size;
// 剩下的节点数为0,那么当前就是最后一组节点
if (n == 0) {
return queue;
}
for (int i = 0; i < size; i++) {
// 从队列中取出一个元素curt
int curt = queue.poll();
// 把每个叶子节点的邻居节点的入度减1
List<Integer> neighbors = graph.get(curt);
for (int next : neighbors) {
// 双向入度减1
indegree.put(next, indegree.get(next) - 1);
indegree.put(curt, indegree.get(curt) - 1);
// 当节点入度为1时,放入queue(新的叶子节点)
if (indegree.get(next) == 1) {
queue.offer(next);
}
}
}
}
return queue;
}
分析
时间复杂度O(V + E),空间复杂度O(V + E)。V代表图的节点数。E代表图的边数。
本题并不是单纯地套用拓扑排序算法,而是使用拓扑排序的思路,实现上更接近BFS层级遍历算法。难度不高,但要求知识点融会贯通。
总结
本章我们学习了图类题中的经典考察模板:拓扑排序。并且联系了BFS层级遍历算法,与拓扑排序进行比较。希望读者能够掌握这两种算法的内核,而不是背下解题模板。
习题
- 课程规划:现在你总共有n门课需要选,记为 0 到 n - 1. 一些课程在修之前需要先修另外的一些课程,比如要学习课程0你需要先学习课程1,表示为[0,1]。给定n门课以及他们的先决条件,判断是否存在有效的选课顺序。
- 全部课程规划顺序:现在你总共有n门课需要选,记为 0 到 n - 1. 一些课程在修之前需要先修另外的一些课程,比如要学习课程0你需要先学习课程1,表示为[0,1]。给定n门课以及他们的先决条件,返回所有有效的选课顺序。