Day 22 Array 数组
章节导读
上一章我们学习了滑动窗口这种技巧,滑动窗口会沿着固定的方向,在一维数组(或者字符串string)上移动。在二维数组上有一种类似的题型,区间类问题。区间类问题一般基于嵌套数组(二维数组),每个单独的数组代表一个区间(时间点、位移、位置…),需要我们按照一定顺序遍历区间,同时进行添加、删除、查询等等操作。
核心算法——区间合并
区间合并类问题有两个基本元素:
- 正方向的描述:正方向可以是时间、位置、起止点等概念
- 区间:每个区间必须是闭合的,有开始有结束
给出a、b两个不同的区间,它们之间有多种可能的情况。我们根据给定的正方向,将区间给定先后顺序,可以将分类简化。
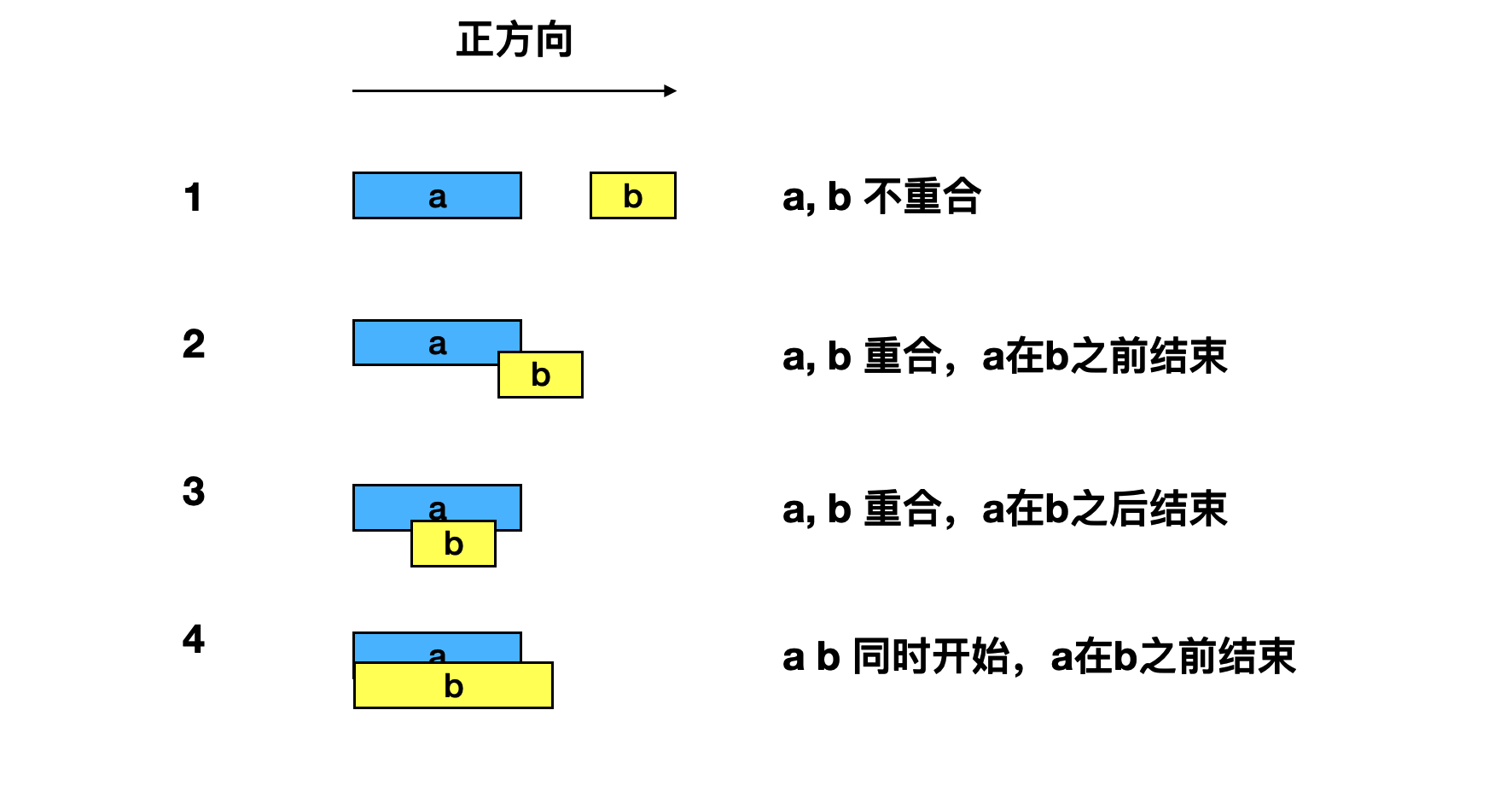
1.案例: 合并区间
给出多个闭合区间,合并所有重叠的部分。
输入: [[1,4], [2,5], [7,9]] 输出: [[1,5], [7,9]]
思路分析
我们先根据题意画出示意图,示例中区间[1,4]和[2,5]有重合部分,所以合并成了区间[1,5]
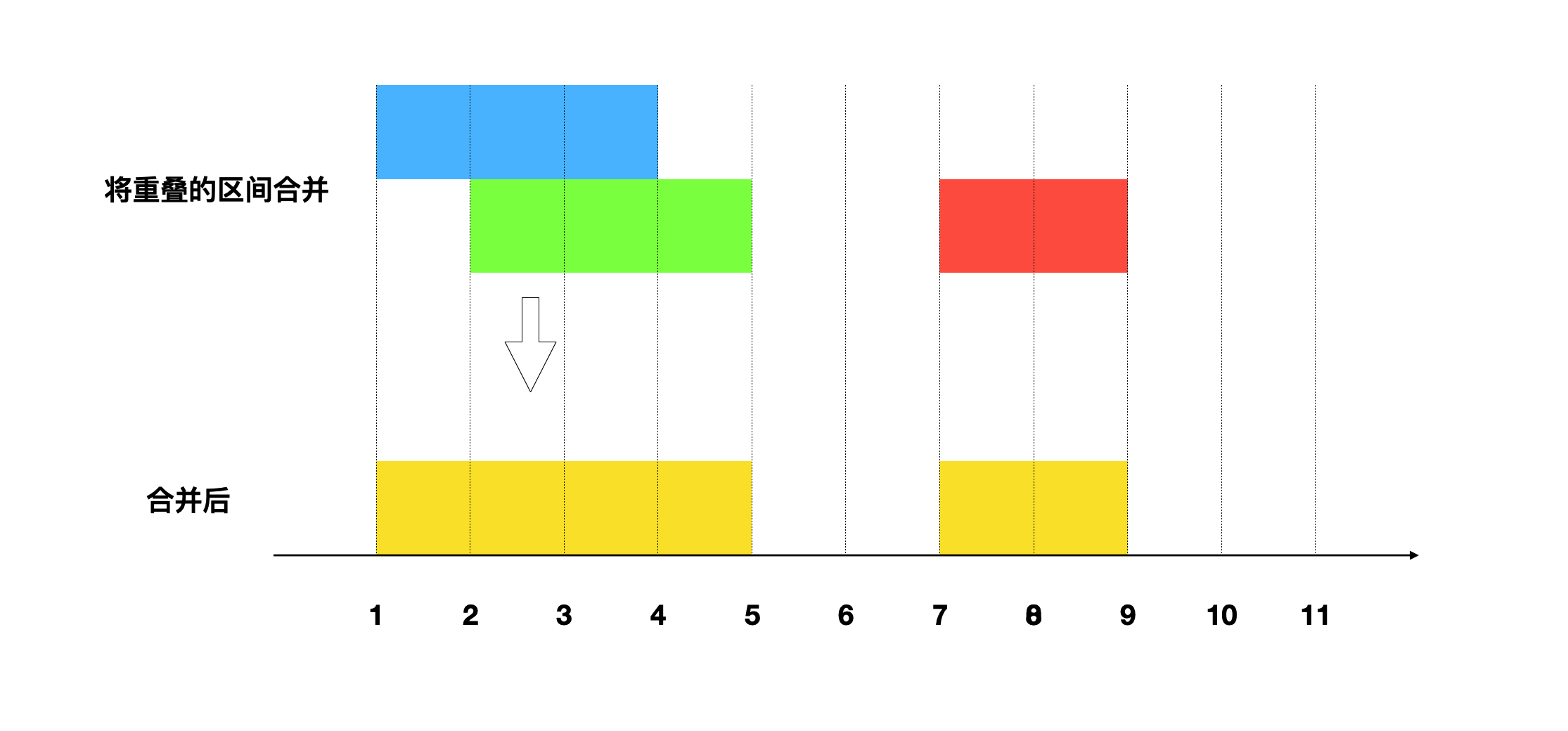
不难看出,区间合并的四种情况中有三种是可以合并的。合并后的区间起点是两个原有区间的最小值,终点是原有区间的最大值。
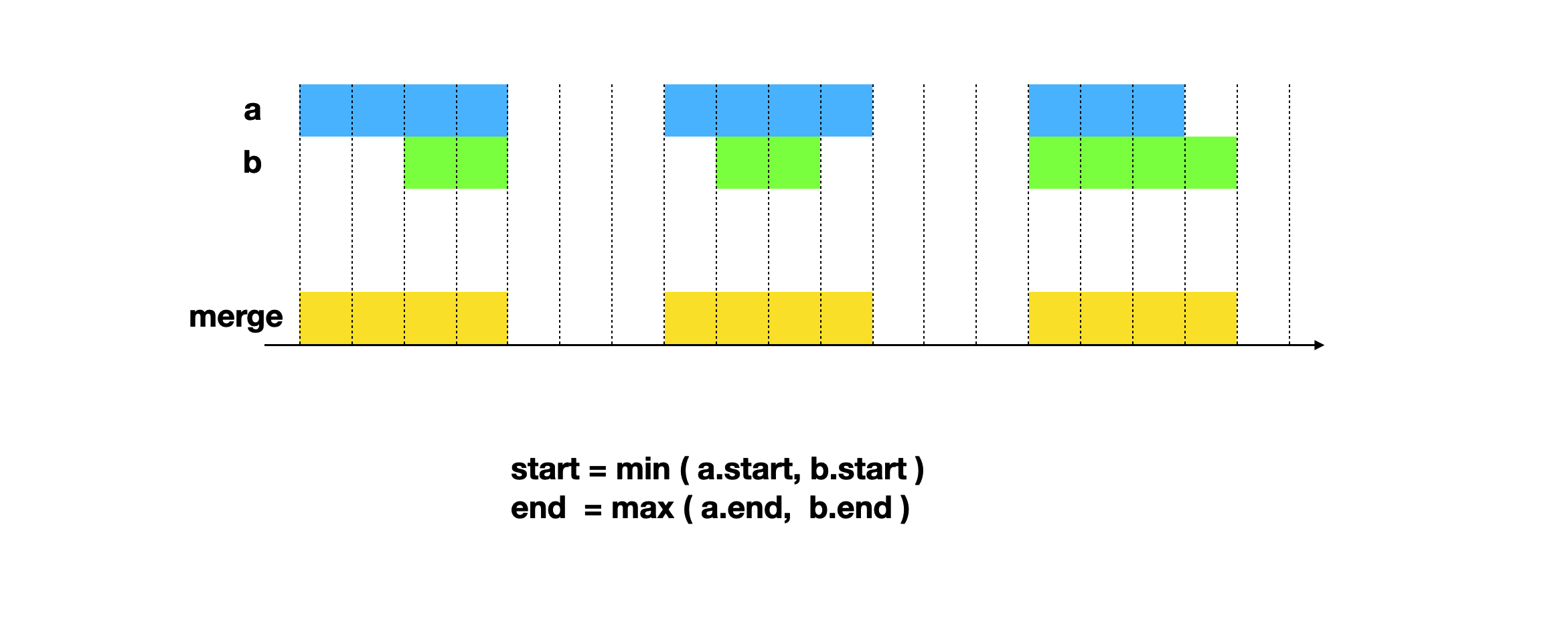
我们可以先将区间按照起点排序,这样就只需要比较终点的值。
- 将区间按照起点排序
- 如果a,b区间重合(b.start <= a.end),那么将a b合并:start = a.start, end = max(a.end, b.end)
- 重复执行步骤2直到结束
代码实现
public int[][] merge(int[][] intervals) {
// 将区间按照起点排序
// 数组第0位是起点,第1位是终点
// 创建Comparator比较器,比较数组第0位
Arrays.sort(intervals, Comparator.comparing(i -> i[0]));
// 建立一个链表记录合并好的结果
LinkedList<int[]> list = new LinkedList<>();
for (int[] i : intervals) {
// 找到上一个区间,如果与当前区间重合(curt.start <= last.end)
if (!list.isEmpty() && i[0] <= list.getLast()[1] ) {
// 合并进前一个区间,start不变,end = max(a.end, b.end)
list.getLast()[1] = Math.max(i[1], list.getLast()[1]);
} else {
// 否则这是一个不需要合并的区间
list.add(i);
}
}
// 返回结果
return list.toArray(new int[list.size()][]);
}
分析
时间复杂度O(n logn),对n个区间排序。空间复杂度O(n),用额外的list保存了结果。
2.案例: 区间交集
给出两组区间,找到两组区间的交集。每组区间之内互不相交,并按照开始时间排序。
输入: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]] 输出: [5, 7], [9, 10]
思路分析
本题是前一题的变种题,画出示意图,这次我们需要的不是两个重叠区间的外边缘,而是内边缘
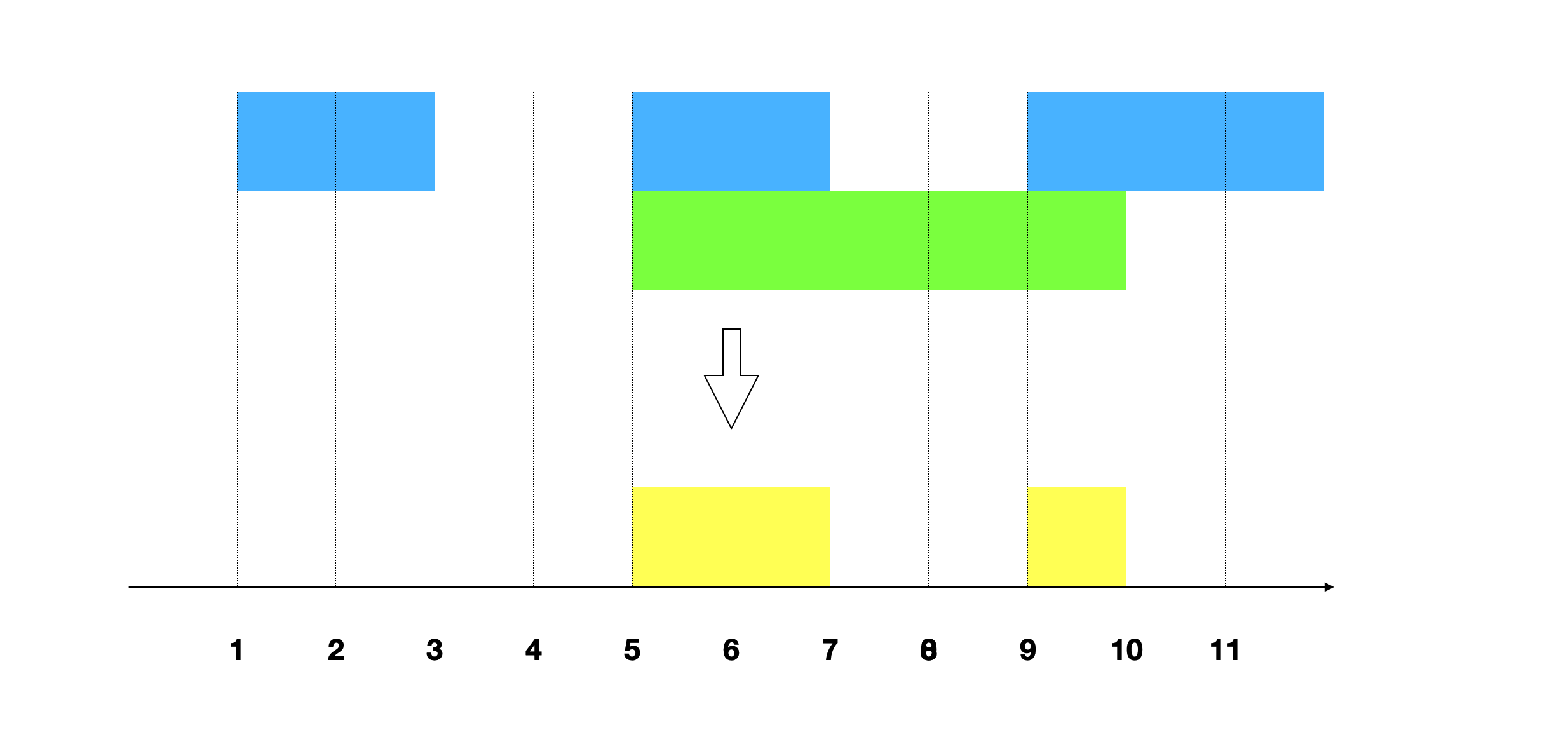
我们可以得出区间合并的规律:
- start = min(a.start, b.start)
- end = max(a.end, b.end)
算法的流程与上一题类似:
- 初始化两个指针,根据区间的结束时间,谁小移谁
- 如果a,b区间重合,那么按规则合并
- 重复执行步骤2直到结束
代码实现
public int[][] intervalIntersection(int[][] A, int[][] B) {
// 初始化两个指针
int i = 0, j = 0;
List<int[]> list = new ArrayList<>();
while (i < A.length && j < B.length) {
// a,b区间重合
if (overlap(A[i], B[j]))
// 按规则合并
list.add(intersect(A[i], B[j]));
// 区间的结束时间,谁小移谁
if (A[i][1] < B[j][1]) {
i++;
} else {
j++;
}
}
return list.toArray(new int[list.size()][]);
}
// 判断区间a,b是否有交集
private boolean overlap(int[] a, int[] b) {
return a[0] < b[0] ? a[1] >= b[0] : overlap(b, a);
}
// 计算区间a,b的交集
private int[] intersect(int[] a, int[] b) {
return new int[]{Math.max(a[0], b[0]), Math.min(a[1], b[1])};
}
分析
时间复杂度O(n),输入的区间已经排序好了,只需要遍历一遍,无需额外排序。空间复杂度O(n),用额外的list保存了结果。
3.案例: 最少会议室
给定一系列的会议时间间隔,包括起始和结束时间[[s1,e1],[s2,e2],…] (si < ei),计算所需的最少会议室数量。
输入: [[4,5], [2,3], [2,4], [3,5]] 输出: 2
思路分析
先根据范例画出示意图,如果之间应用区间合并算法,我们会发现所有的区间都合并进了[2,5],这表示4个区间重合。
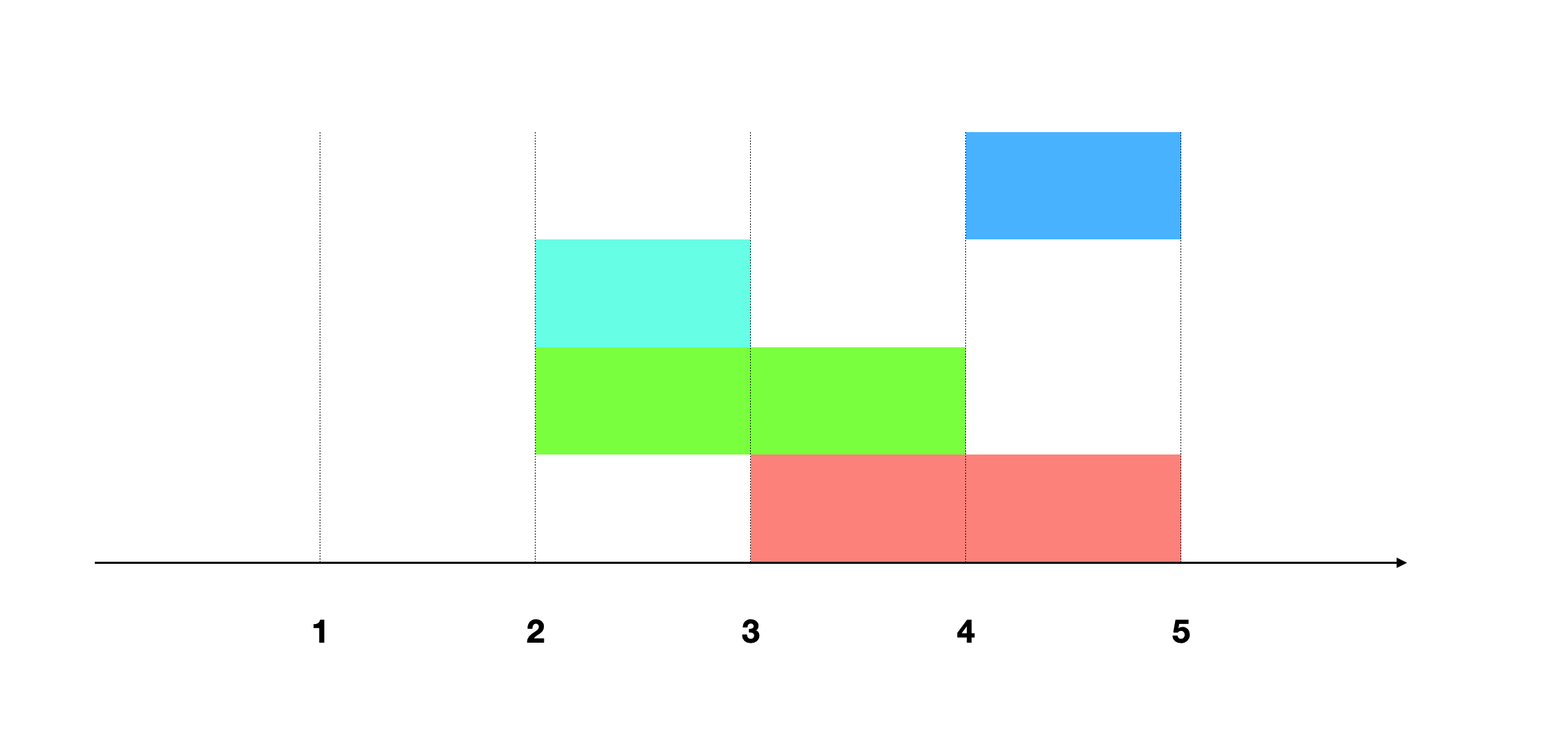
实际上我们并不需要4个会议室,[2,3]与[3,5]并不重合,因此我们只需要记录互斥的会议个数。仅当两个会议互斥时,才新增一个会议室。我们需要同时利用会议的开始时间和结束时间两个信息。先将会议按照开始时间排序,每一个会议开始时,我们要检查有多少会议还没有结束。
- 将会议按照开始时间排序
- 初始化一个最小堆,按照结束时间排序当前正在进行的会议
- 遍历所有会议,每一个会议开始时,我们要检查有多少会议正在进行
- 将已经结束的会议从最小堆弹出
- 计算当前正在进行的会议
- 重复3 - 5,直至结束
代码实现
public int minMeetingRooms(int[][] intervals) {
// 将会议按照开始时间排序
Arrays.sort(intervals, Comparator.comparing(i -> i[0]));
int minRoom = 0;
// 初始化一个最小堆,按照结束时间排序当前正在进行的会议
// 创建Comparator比较器,比较数组第1位,即结束时间
PriorityQueue<int[]> minHeap = new PriorityQueue<>(Comparator.comparing(i -> i[1]));
// 遍历所有会议
for (int[] i : intervals) {
// 加入当前会议
minHeap.offer(i);
// 将已经结束的会议从最小堆弹出
while (!minHeap.isEmpty() && minHeap.peek()[1] <= i[0])
minHeap.poll();
// 计算最多需要多少个会议室
minRoom = Math.max(minRoom, minHeap.size());
}
return minRoom;
}
分析
时间复杂度O(n logn),对n个区间排序。空间复杂度O(n),用额外的heap
4.案例: 空闲时间
有k个工作人员,用一个二维列表表示他们的工作时间。找到所有员工共同的空闲时间。当前的工作时间已经按开始时间排序
输入: [[[1,3], [9,12]], [[2,4]], [[6,8]]] 输出: [4,6], [8,9]
思路分析1
我们可以按照区间合并的思路来解决本题
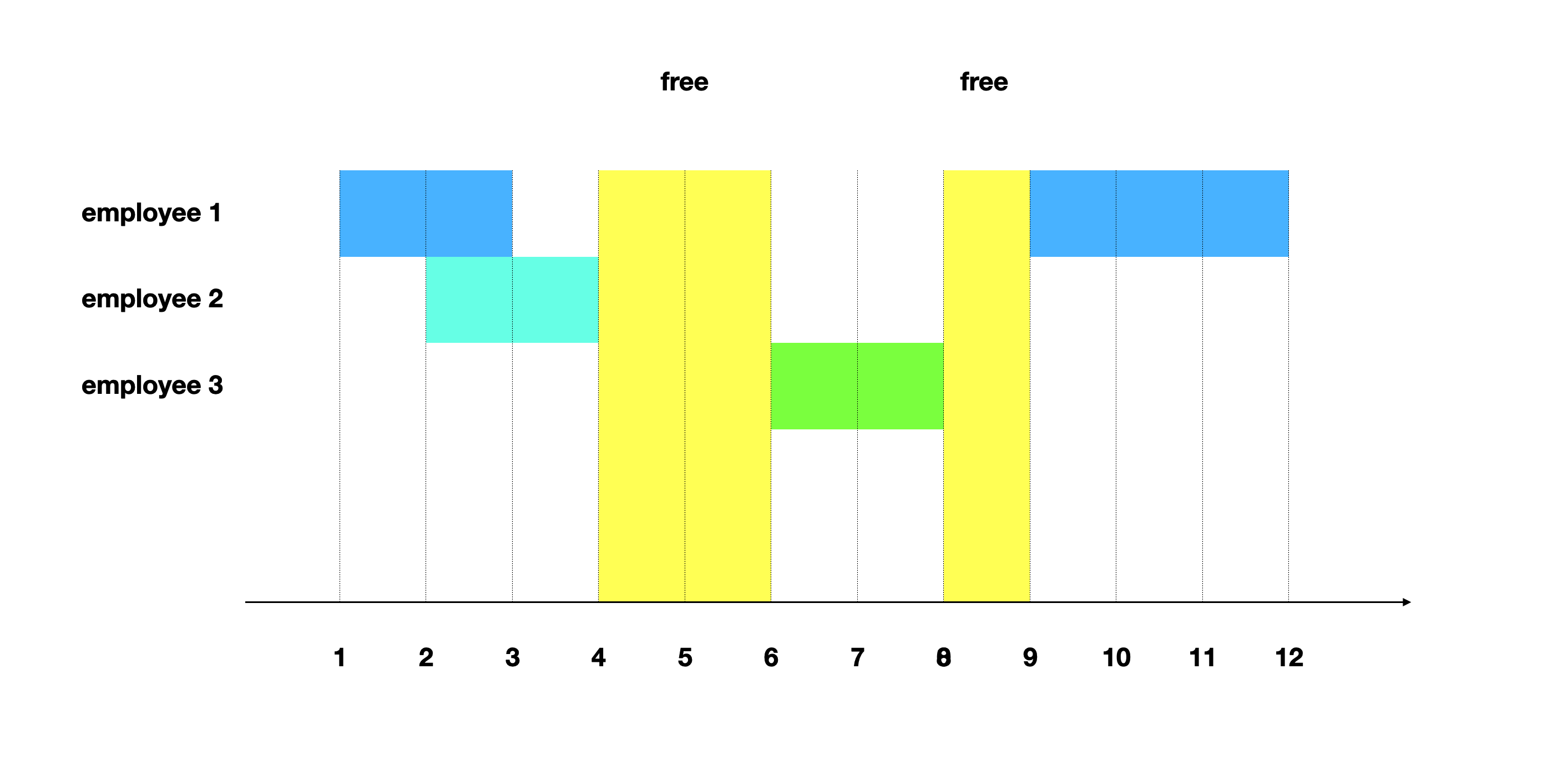
- 将所有区间按开始时间排序
- 将重叠的区间合并
- 找到合并后的区间之间的间隔
代码实现1
public List<Interval> employeeFreeTime(List<List<Interval>> schedule) {
// 获得所有区间
List<Interval> flatten = new ArrayList<>();
for (List<Interval> s : schedule) {
flatten.addAll(s);
}
// 将所有区间按开始时间排序
Collections.sort(flatten, Comparator.comparing(i -> i.start));
// 将重叠的区间合并
LinkedList<Interval> list = new LinkedList<>();
for (Interval i : flatten) {
if (!list.isEmpty() && i.start <= list.getLast().end ) {
list.getLast().end = Math.max(i.end, list.getLast().end);
} else {
list.add(i);
}
}
List<Interval> ans = new ArrayList<>();
// 找到合并后的区间之间的间隔
for (int i = 1; i < list.size(); i++) {
int start = list.get(i - 1).end;
int end = list.get(i).start;
ans.add(new Interval(start, end));
}
return ans;
}
思路分析2
解法1需要O(n logn)的时间复杂度消耗和O(n)的空间复杂度消耗,尤其是我们创建了三个列表来缓存中间结果。
我们其实在之前的章节中见过类似的题目:链表的k路合并。本题更像是k路合并在区间上的应用。
我们创建一个Node class,来完成k路合并。Node包含了当前的区间,相关的员工eid,和对应员工工作时间的下标。
class Node {
Interval interval;
int eid, idx;
public Node(Interval interval, int eid, int idx) {
// 当前的区间
this.interval = interval;
// 员工eid
this.eid = eid;
// 对应工作时间的下标
this.idx = idx;
}
}
- 创建一个最小堆,按照开始时间排序
- 将每个员工的第1段工作时间加入最小堆
- 从最小堆中取出最早的区间,记下它的结束时间
- 每次从最小堆中取出一个区间,与当前已知的结束时间比较,更新已知的结束时间
- 将Node移至下一位,将下一段工作时间加入最小堆
- 重复3-4,直至结束
代码实现2
public List<Interval> employeeFreeTime(List<List<Interval>> schedule) {
List<Interval> ans = new ArrayList<>();
// 创建一个最小堆,按照开始时间排序
PriorityQueue<Node> minHeap = new PriorityQueue<>((a, b) -> a.interval.start - b.interval.start);
for (int i = 0; i < schedule.size(); i++) {
// 将每个员工的第1段工作时间加入最小堆
minHeap.offer(new Node(schedule.get(i).get(0), i, 0));
}
// 最早区间的结束时间
int lastEnd = minHeap.peek().interval.end;
while (!minHeap.isEmpty()) {
// 每次从最小堆中取出一个区间
Node curt = minHeap.poll();
// 当前区间的开始时间晚于lastEnd,说明二者不重合,中间有空闲时间
if (curt.interval.start > lastEnd) {
// 获得空闲时间
ans.add(new Interval(lastEnd, curt.interval.start));
}
// 更新已知最晚的结束时间
lastEnd = Math.max(lastEnd, curt.interval.end);
List<Interval> freeTime = schedule.get(curt.eid);
// 如果当前员工还有下一段工作时间,加入最小堆
if (curt.idx + 1 < freeTime.size()) {
minHeap.offer(new Node(freeTime.get(curt.idx + 1), curt.eid, curt.idx + 1));
}
}
return ans;
}
分析
时间复杂度O(n logk),空间复杂度O(k),k是员工总数。最小堆消耗了O(k)空间,并且执行了n次O(logk)的插入与删除操作。
总结
本章我们学习了区间类问题。区间类问题特征比较明显,一般使用嵌套列表或二维数组,每个单独的数组代表一个区间。解法也比较普适,需要我们按照一定顺序(起点或者终点)排序,然后遍历所有区间。
习题
- 给定一系列的会议时间间隔,包括起始和结束时间[[s1,e1],[s2,e2],…] (si < ei),判断一个人是否可以参加所有会议。
- 给定一些区间,找到需要移除的最小区间数,以使其余的区间不重叠。
- 给出一个无重叠的按照区间起始端点排序的区间列表。在列表中插入一个新的区间,你要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。