Day 23 Array 数组
章节导读
数组类问题中,搜索是最常见的问题之一。面试官通常会给出一个数组、链表或者矩阵,然后要求面试者高效地查询特定元素。这一类问题中,最经典的解法就是二分法。二分法思路简单,但是非常高效,并且能有效考察面试人员的编码水平。
核心算法——二分搜索算法
二分搜索法是一种经典的算法,能在有序数组中以O(logn)的效率搜索特定的元素。
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果给定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找。这种搜索算法每一次比较都使搜索范围缩小一半。
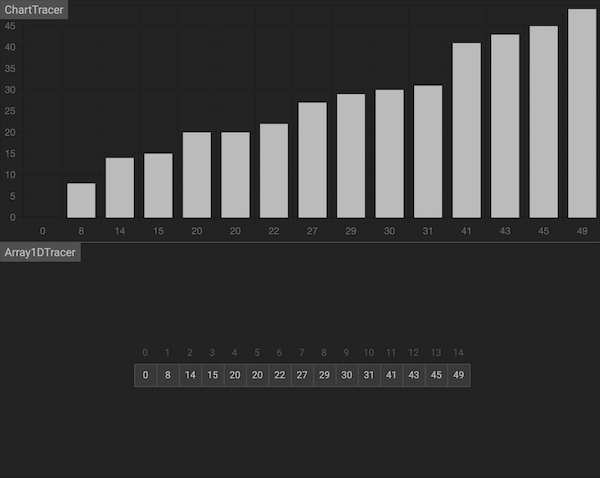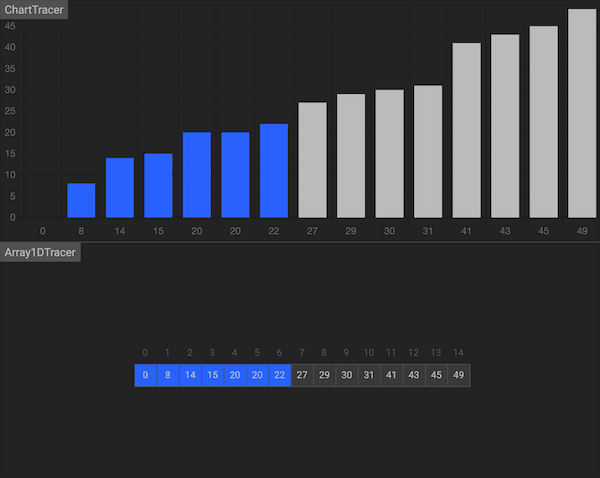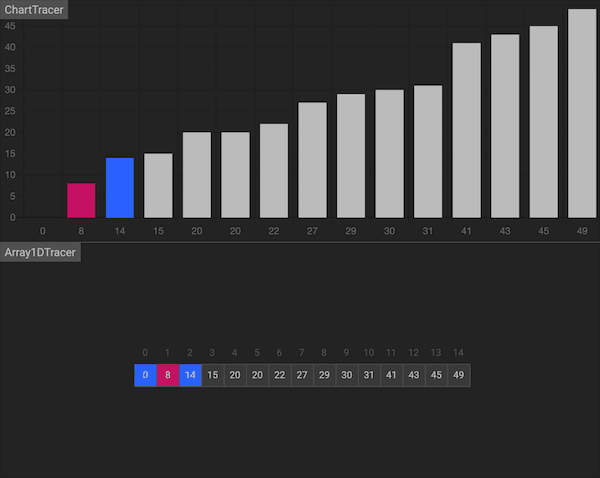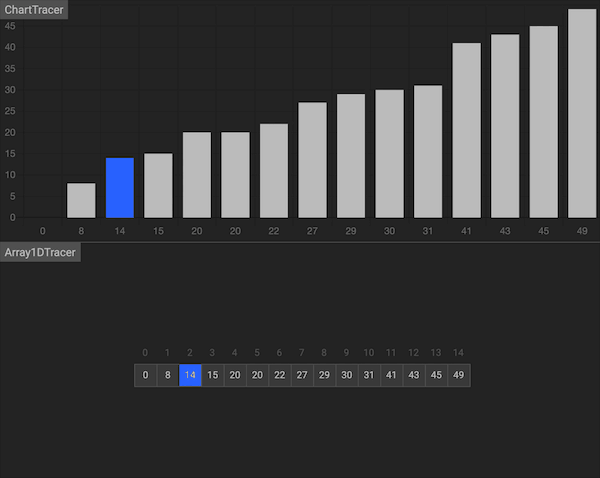
图片由algorithm-visualizer制作
二分搜索算法:
- 初始化left和right,分别指向首位和末位
- 找到中间位置mid
- 如果mid不是我们要找到target 3.1. 如果target比mid指向的值小,说明target的位置在mid左侧,更新right的值 3.2. 如果target比mid指向的值大,说明target的位置在mid右侧,更新left的值
- 如果mid指向我们要找到target,返回mid的值
- 重复2-4步,直到退出循环
实际上,二分搜索不只对有序数组有效,任何有序的可比较的集合都可以纳入二分法的适用范围,比如习题2的适用二分法开平方。
1.案例: 二分搜索法
给定一个已排序的数组,找到target对应的下标。如果target不存在,返回-1
输入: nums = [0, 1, 21, 33, 45, 45, 61, 71, 72, 73], target = 33 输出: 3
思路分析1
二分法的思路虽然简单,但是90%的人并不能将它写对,很多人甚至会在边界条件上花上好几个小时。根据高德纳在《计算机程序设计的艺术》中所说:1946年就有公开发布的二分法算法,但是直到1962年才有人写出没有bug的二分法程序。
这里我们先一段曾经java内置的binarySearch算法为例,分析二分法的实现难点。为了简化流程,我对它做了一些修改。
代码实现1
public int search(int[] nums, int target) {
// 指定搜索范围
int left = 0, right = nums.length - 1;
while (left <= right) {
// 找到中间位置
int mid = (left + right) / 2;
if (nums[mid] == target) { // 找到目标元素
return mid;
} else if (nums[mid] < target) { // 目标元素在mid右侧
left = mid + 1; // 抛弃mid左侧的搜索范围
} else { // 目标元素在mid左侧
right = mid - 1; // 抛弃mid右侧的搜索范围
}
}
// 未找到目标元素
return -1;
}
这段代码来自乔恩·本特利的《编程珠玑》,其中第6行存在整数溢出的问题,并且超过20年无人察觉。本特利也是java语言库的贡献者,这段有bug的代码在java中存在9年才被修复。
第6行
int mid = (left + right) / 2;
如果left和right都是很大整数,二者相加超过了整数范围的上限,那么就会导致整型溢出错误。 本特利2006年在自己的博客中表示这里应该改成
int mid = left + (right - left) / 2;
但是同时他表示,自己依然不能确定这段代码已经没有bug了。(其实2008年,他还真的又找到了一个bug)
思路分析2
将二分法的算法变成代码实现,这个过程中存在太多模糊的地方:
- 如何设置终止条件?应该是 left < right 还是 left <= right ?
- 如何确定边界left和right?
- 如何更新边界?left = mid 还是 left = mid + 1, right = mid 还是 right = mid - 1 ?
- ……
基于以上事实,二分法可以说是最难实现的算法之一。因此要向大家额外介绍一种二分法的模板,这段模板可以避免off-by-one error。
代码实现2
public int search(int[] nums, int target) {
// 指定搜索范围
int left = 0, right = nums.length - 1;
// 放宽结束条件
while (left + 1 < right) {
// 避免整型溢出
int mid = left + (right - left) / 2;
if (nums[mid] == target) { // 找到目标元素
return mid;
} else if (nums[mid] < target) { // 目标元素在mid右侧
// 放宽边界收缩
left = mid;
} else { // 目标元素在mid左侧
// 放宽边界收缩
right = mid;
}
}
// 通过额外的两次比较判断边界
if (nums[left] == target) return left;
if (nums[right] == target) return right;
// 未找到目标元素
return -1;
}
这段模板通过放宽边界来避免off-by-one error。每次边界的更新相对宽松,仅仅将mid的值赋值给left和right。所以当终止条件 left + 1 < right 达成时,还有两个元素未被访问。此时再通过额外两次比较从left和right中找到目标元素。
分析
时间复杂度O(logn),空间复杂度O(1)。二分法存在多种模板,但是没有人可以保证某种模板适用于所有题型,读者在面试时需要根据题目自行调整算法。
2.案例: 数字范围
给定一个升序数组nums和一个值target。找出target在nums中的开始位置和结束位置。如果不存在,返回[-1, -1]。
输入: [4, 6, 6, 6, 9], 6 输出: [1, 3]
思路分析
本题是在二分搜索法上的延伸,我们只需要扩展二分法的第四步算法,让它适应搜索开始位置和结束位置两种模式。
- 初始化left和right,分别指向首位和末位
- 找到中间位置mid
- 如果mid不是我们要找到target 3.1. 如果target比mid指向的值小,说明target的位置在mid左侧,更新right的值 3.2. 如果target比mid指向的值大,说明target的位置在mid右侧,更新left的值
- 如果mid指向我们要找到target 4.1. 要找到第一个出现的target,我们更新right的值,来寻找左侧(mid之前)出现的target 4.2. 要找到最后一个出现的target,我们更新left的值,来寻找右侧(mid之后)出现的target
- 重复2-4步,直到退出循环
代码实现
public int[] searchRange(int[] nums, int target) {
int[] ans = new int[]{-1, -1};
if (nums == null || nums.length == 0)
return ans;
// 分别找到target在nums中的开始位置和结束位置
ans[0] = find(nums, target, true);
ans[1] = find(nums, target, false);
return ans;
}
int find(int[] nums, int target, boolean first) {
// 初始化left和right,分别指向首位和末位
int idx = -1, left = 0, right = nums.length - 1;
while (left <= right) {
// 找到中间位置mid
int mid = left + (right - left) / 2;
if (target < nums[mid]) { // 如果target比mid指向的值小
// 更新right的值
right = mid - 1;
} else if (nums[mid] < target) { // 如果target比mid指向的值大
// 更新left的值
left = mid + 1;
} else { // mid指向要找到target
// 记录下当前的下标
idx = mid;
if (first) { // 寻找第一个出现的target
// 更新right的值,寻找mid之前出现的target
right = mid - 1;
} else { // 寻找最后一个出现的target
// 更新left的值,寻找mid之后出现的target
left = mid + 1;
}
}
}
// 返回idx记录的下标
return idx;
}
分析
时间复杂度O(logn),空间复杂度O(1)
3.案例: 二分查找无限长度升序数组
给定一个无限长度的升序数组,找到数组中是否存在target的值。如果存在,返回target的下标;否则返回-1。(提供ArrayReader.get(index)接口来查询)
输入: [4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30…], target = 16 输出: 6
思路分析
本题代表了二分搜索的一个变种:当题目没有给定搜索边界时,如何进行搜索。
我们反向利用二分法的思路,通过每次翻倍边界向外扩张,直到找到一个有效的边界。
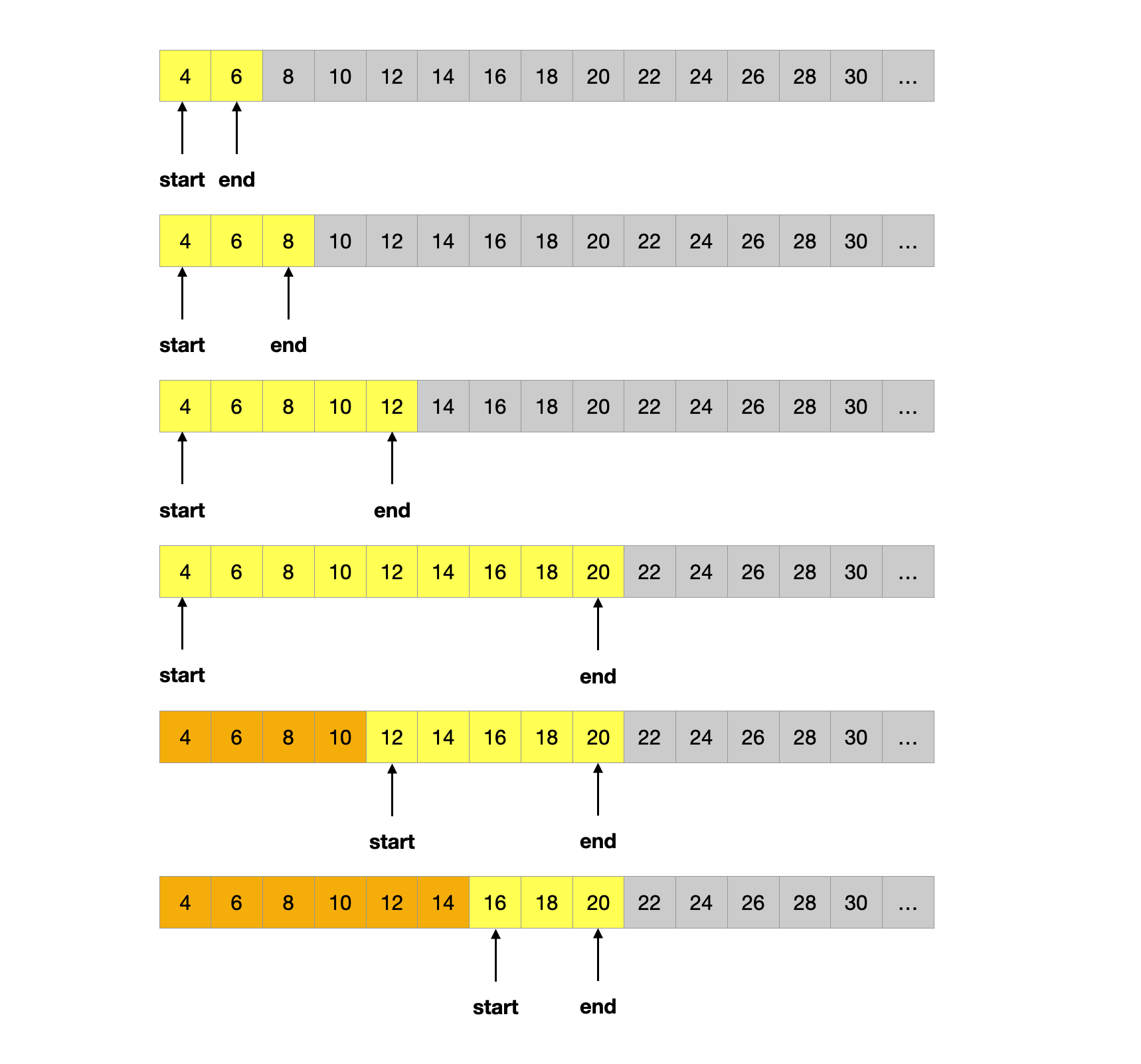
一旦确定了上下边界,我们再向内收缩,使用二分法查找。
代码实现
public int search(ArrayReader reader, int target) {
// 初始化上下边界
int start = 0, end = 1;
// 持续翻倍边界向外扩张,直到将target包含边界内
while (reader.get(end) < target)
end *= 2;
// 在上下边界内,使用二分法查找。
while (start <= end) {
int mid = start + (end - start) / 2;
if (reader.get(mid) == target) {
return mid;
} else if (reader.get(mid) < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return -1;
}
分析
时间复杂度O(logn),空间复杂度O(1)
4.案例: 搜索旋转排序数组
给定一个旋转排序数组nums和一个值target,找出target在nums中的索引,否则返回-1。
输入: [4, 5, 7, 9, 10, -1, 2], 10 输出: 4
思路分析
本题是二分搜索的另一个变种:在旋转数组上搜索。旋转数组在局部上依然保持了升序的性质,仅在部分地方造成了中断。对于这类题目,我们依然使用二分法的思路,但是要在升序中断的地方做出相应的修改。
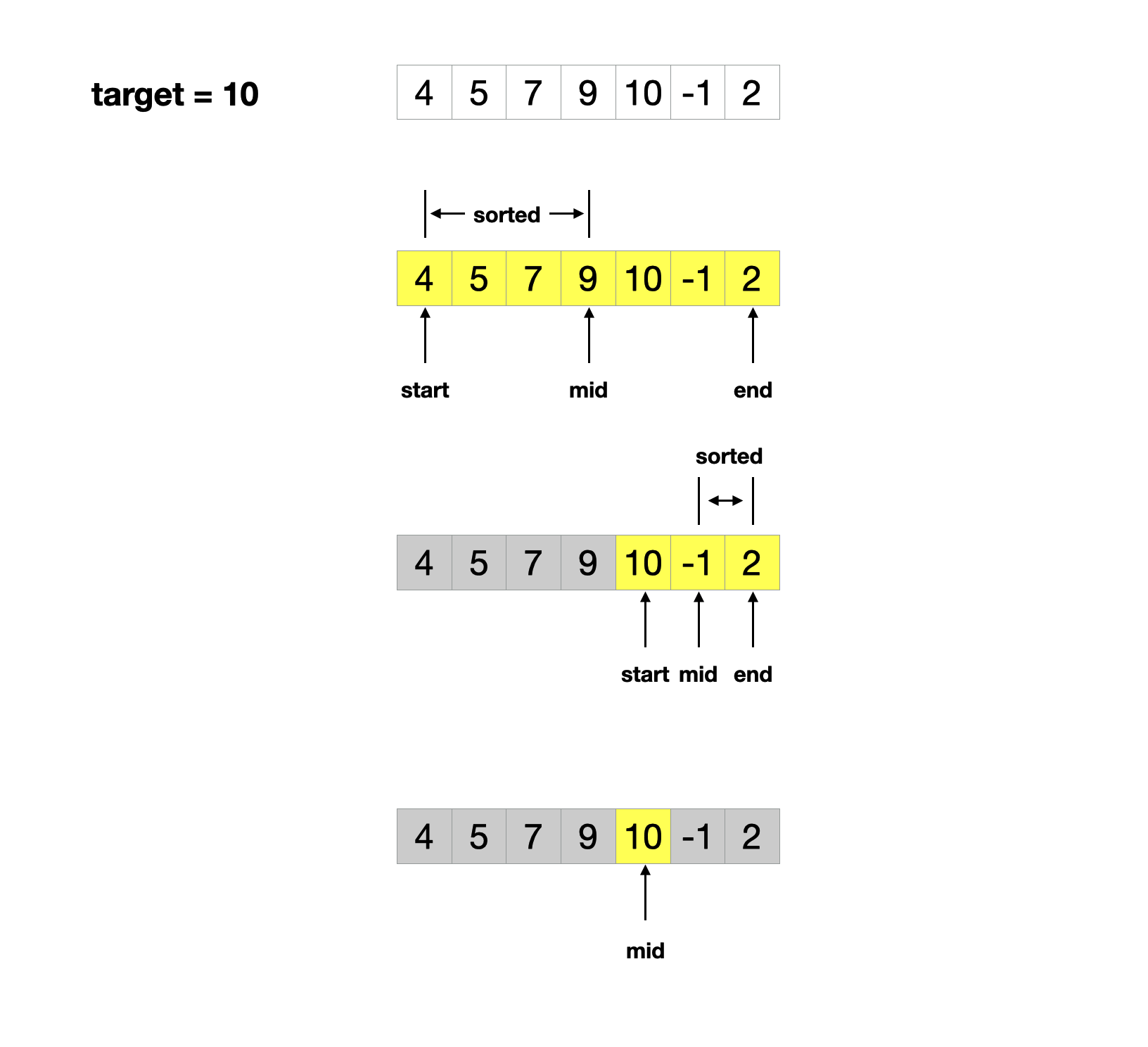
- 初始化left和right,分别指向首位和末位
- 找到中间位置mid
- 如果mid指向我们要找到target,返回mid
- 如果mid不是我们要找到target,判断保持升序的部分 4.1. 如果nums[left] <= nums[mid],说明left到mid之间依然保持升序 4.2. 否则,说明mid到right之间保持升序
- 判断target是否位于保持升序的区间内,更新对应的边界
- 重复2-5步,直到退出循环
代码实现
public int search(int[] nums, int target) {
// 初始化left和right,分别指向首位和末位
int left = 0, right = nums.length - 1;
while (left <= right) {
// 找到中间位置mid
int mid = (left + right) / 2;
// 找到目标元素,返回mid
if (nums[mid] == target) {
return mid;
}
if (nums[left] <= nums[mid]) { // 说明[left, mid]保持升序
// target位于[left, mid]内
if (nums[left] <= target && target <= nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else { // 说明[mid, right]保持升序
// target位于[mid, right]内
if (nums[mid] <= target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
分析
时间复杂度O(logn),空间复杂度O(1)
总结
本章我们学习了二分法和它的变种。二分法思路简单,但是在实现过程中会有很多暗藏的bug。想要一次性写出bug-free的版本,还需要读者多加练习。
习题
- 给定一串排序的letters小写字母数组,给定一个目标字母target,找出letters中大于目标字母的最小字母。
- 实现int sqrt(int x)函数,计算并返回x的平方根。
- 给定一个旋转排序且可能有重复值的数组nums和一个值target,找出target在nums中的索引,否则返回-1。