Day 24 String 字符串 4
之前我们已经学习了很多数组上的解题技巧:两根指针、滑动窗口等,这些技巧同样可以应用在string类题目上。有的读者可能会将string类问题当成单独的一个分类,其实并无必要。String类问题应当看成数组类问题的延伸,我们会在接下来的章节里介绍在string上使用动态规划、pattern match等高级技。在这些题中string和数组的区别非常模糊,我们可以认为他们就是等价的。
1.案例: 字符串查找
对于给定字符串s1和s2,返回s2在s1中出现的第一个位置。如果不存在,则返回-1。
输入: s1 = “abcdabcdefg”,s2 = “bcd” 输出: 1
思路分析1
本题是字符串类问题中最经典的一道题,要求判断一个字符串是否包含另一个字符串。这种题目存在很多经典的算法,有些算法本身已经包含在内置函数中。比如java中就内置了indexOf函数,实现了KMP算法,能够在O(n)的时间内得出结果。
即使不知道KMP算法也并不是问题,本题的暴力解法也很容易想到,消耗了O(n2)的时间。如果在面试时遇到这样的题目,那么重点应该放在bug-free和沟通上。先向面试官提出暴力解法,并写出代码,然后再根据面试官的要求进行优化。
brute froce:
- 在s1的每一个位置,尝试与s2进行匹配
- 如果当前位置的s1的子字符串不能匹配上s2,那么移到下一位
- 如果匹配成功返回当前坐标
- 直到s1结尾都没有匹配成功,返回-1
代码实现1
public int strStr(String haystack, String needle) {
if (needle.length() == 0) {
return 0;
}
for (int i = 0; i < haystack.length() - needle.length() + 1; i++) {
// 在s1的每一个位置,尝试与s2进行匹配
if (check(haystack, i, needle))
return i; // 匹配成功返回当前坐标
}
//直到s1结尾都没有匹配成功,返回-1
return -1;
}
private boolean check(String haystack, int idx, String needle) {
// 将s1的子字符串的每一位与s2比较
for (int i = 0; i < needle.length(); i++) {
if (haystack.charAt(idx + i) != needle.charAt(i)) return false;
}
return true;
}
思路分析2
KMP算法并不常见,并且用处有限。以致于面试者如果在面试中真的写出了KMP算法,反倒会被怀疑背过答案。这里介绍Robin Karp解法,利用了滑动窗口和hash的思路,也能够在O(n)的时间内得出结果,与KMP算法一样高效。
首先我们要将字符串当成数组来理解,将原题简化: 给出数组num1 = [1, 2, 3, 4, 5, 6]和num2 = [3, 4, 5],判断数组num1是否包含num2.
对于简化后的题目,我们马上能够判断出,应该将数组转化成等价的数字来处理。 我们按照十进制的算法将nums2转化成数字:[3, 4, 5] = 3 * 102 + 4 * 101 + 5 * 100 = 345。我们将这个数字称为num2的指纹fingerprint。
然后我们利用滑动窗口的方法,在num1上滑动,并且每次将子数组转化成数字hash,代表子数组的对应数字。当滑动窗口移动的时候,我们需要做两件事:
- 将之前的数字x10,并加上新的数字
- 将最高位的数字x103,从新的数字中减去
我们将第二步中103称为bound,代表最高位的权重。比如从[1, 2, 3]移动到[2, 3, 4]时,通过这两步变化,我们可以在O(1)的时间内,得到新的值
- 123 * 10 + 4 = 1234
- 1243 - 1 * 103 = 234
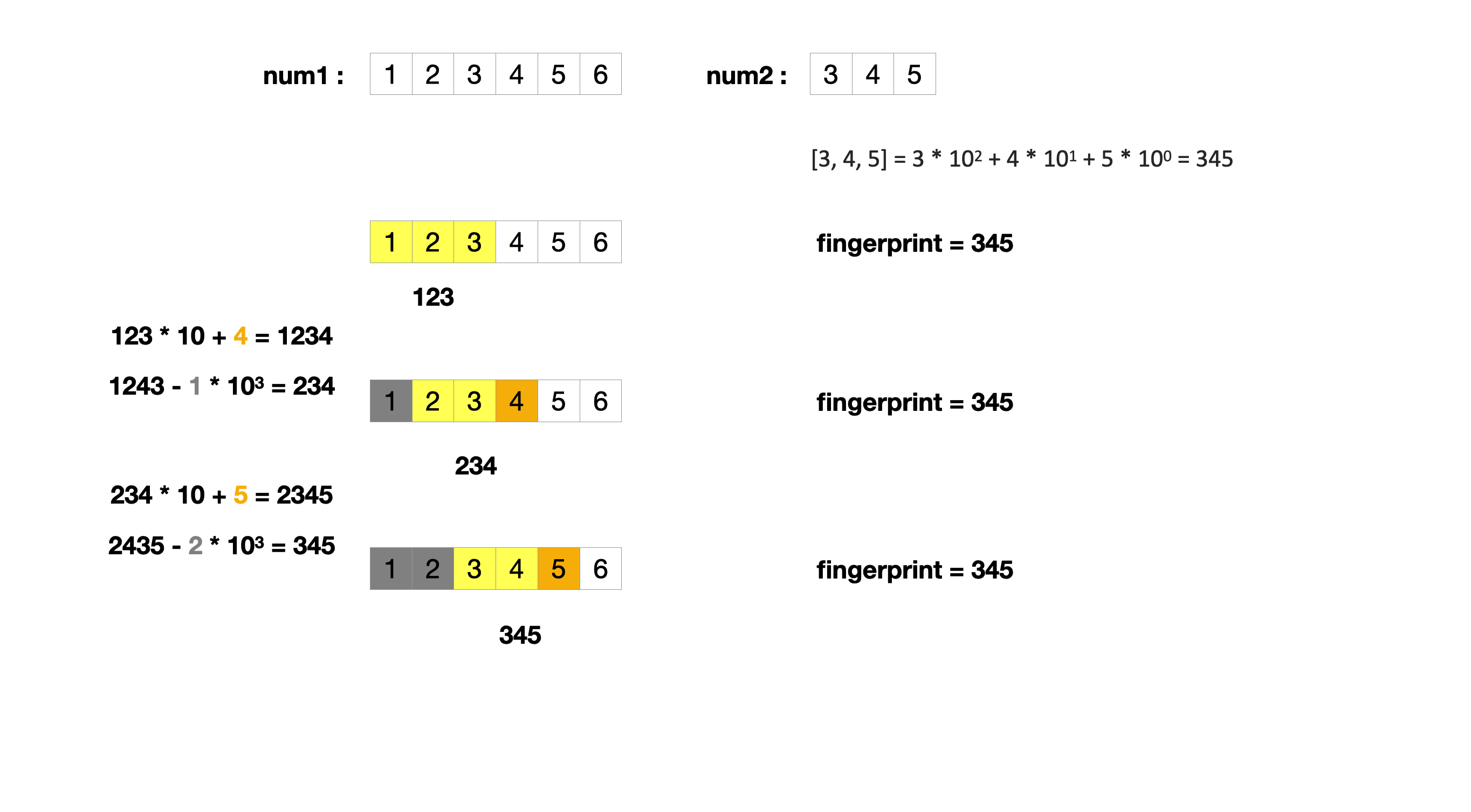
重复上面的步骤,我们可以在index=2时,找到num2在num1中的对应位置。这就是Robin Karp算法的基本思路。
现在我们回到字符串,将字母a-z看做0-25的数字,那么字符串就对应了一个26进制的数字。
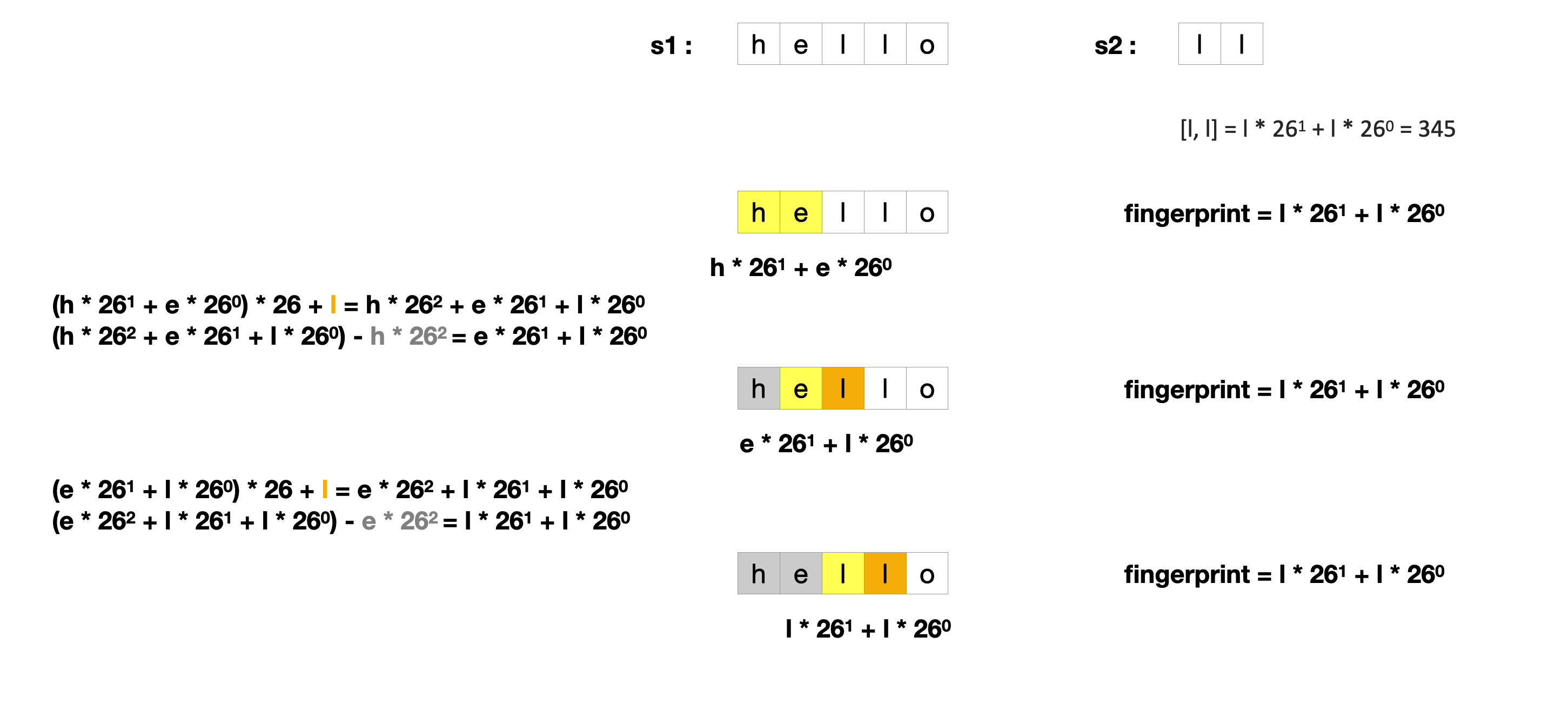
我们只需要对上面的思路做一点修改:
- 将字母a-z看做0-25的数字,将字符串成一个字母数组,再转化成一个26进制的数字
- 对这个数字取余,防止整型溢出。取余的数字需要足够大。(有乘法必定取余;有减法,加上mod后取余)
- 因为我们使用了取余,节省了空间。当hash等于fingerprint时,我们还需要额外进行验证,防止hash碰撞
代码实现2
public int strStr(String s1, String s2) {
if (s2.length() == 0) return 0;
if (s2.length() > s1.length()) return -1;
// 将字符串看做26进制的数字
int base = 26;
// 设置一个取余的数字,防止整型溢出
int mod = 9997;
int bound = 1, fingerprint = 0, hash = 0;
for (int i = 0; i < s2.length(); i++) {
// 计算出s2的fingerprint
fingerprint = (fingerprint * base + s2.charAt(i) - 'a') % mod;
// 计算出s1子字符串的hash
hash = (hash * base + s1.charAt(i) - 'a') % mod;
// 计算出最高位的权重bound
bound = bound * base % mod;
}
for (int i = 0; i <= s1.length() - s2.length(); i++) {
// 当hash等于fingerprint时,进行额外进行验证
if (hash == fingerprint && check(s1, i, s2))
// 如果找到,返回当前坐标
return i;
// 退出循环
if (i == s1.length() - s2.length()) break;
// 将之前的数字 * base,并加上新的数字
hash = (hash * base + s1.charAt(i + s2.length()) - 'a') % mod; // 有乘法必定取余
// 将最高位的数字 * bound,从新的数字中减去
hash = (hash + mod - (s1.charAt(i) - 'a') * bound % mod) % mod; // 有减法,加上mod后取余
}
return -1;
}
分析
时间复杂度O(n),空间复杂度O(1)
2.案例: 最长回文子串
给出一个字符串,求出它的最长回文子串。
输入: abaxyzzyxf 输出: xyzzyx
思路分析
本题与上一题类似存在已知且有效的算法。上一题Robin Karp解法因为使用了滑动窗口的思路,还算值得学习。本题的算法用处有限也不常见,因此不值得刻意背算法。应该先向面试官提出暴力解法,并写出代码,然后再根据面试官的要求进行优化。
本题的暴力解法也很容易想到,消耗了O(n2)的时间。即在每一个位置向两侧扩展,判断当前位置上的回文子串长度。最后找到全局最长的回文子串。
需要注意的是,回文子串有两种:
- 长度为奇数,如果aba
- 长度为偶数,如果abba
代码实现
public String longestPalindrome(String s) {
int start = 0, len = 0, longest = 0;
// 在每个位置判断当前位置上的回文子串长度
for (int i = 0; i < s.length(); i++) {
// 假设回文子串长度为偶数,计算当前位置的回文子串长度
len = find(s, i, i + 1);
if (len > longest) { // 与当前最长长度比较
// 更新长度与起始位置
longest = len;
start = i - len / 2 + 1;
}
// 假设回文子串长度为奇数,计算当前位置的回文子串长度
len = find(s, i, i);
if (len > longest) { // 与当前最长长度比较
// 更新长度与起始位置
longest = len;
start = i - len / 2;
}
}
return s.substring(start, start + longest);
}
private int find(String s, int left, int right) {
// 从给定的初始位置,向左右扩展,计算最长回文子串的长度
while (left >= 0 && right < s.length()) {
if (s.charAt(left) != s.charAt(right)) {
break;
}
left--;
right++;
}
return right - left - 1;
}
分析
时间复杂度O(n2),空间复杂度O(1)
3.案例: 异位词分组
给定一个字符串数组, 将异位词(指相同字符不同排列的字符串)分组
输入: [“yo”, “act”, “flop”, “tac”, “foo”, “cat”, “oy”, “olfp”] 输出: [[“yo”, “oy”], [“flop”, “olfp”], [“act”, “tac”, “cat”], [“foo”]]
思路分析
本题是一道高频考题,由此可见一部分面试题的难度其实很低。本题的关键在于将单词按照字符分布分类,并且不同单词如果有相同的字符分布,它们应该分到同一类。只要找到一种分类方式就可以解决本题。最简单的方法是将每个单词转化成字符的数组,然后对这个数组排序。将排序后的字符数组重新转化成字符串,作为分类的标准。这样一来,不同分布相同字符的单词就可以分到同一类,比如“ab”和“ba”排序后都是“ab”。
代码实现
public List<List<String>> groupAnagrams(String[] strs) {
// 建立一个map来存储分类
HashMap<String, List<String>> map = new HashMap<>();
// 对每一个字符串
for (String str : strs) {
// 将字符串转化成字符数组
char[] s = str.toCharArray();
// 将字符数组排序
Arrays.sort(s);
// 将排序后的字符数组重新转化成字符串,作为分类的key
String key = new String(s);
map.putIfAbsent(key, new ArrayList<>());
// 将拥有相同key的单词加入同一个列表
map.get(key).add(str);
}
// 返回分类后的结构
return new ArrayList<>(map.values());
}
分析
时间复杂度O(n logk),空间复杂度O(n),k是最长的字符串长度
4.案例: 最长有效括号
给出一个只包含’(‘和’)’的字符串,找出其中最长的左右括号正确匹配的合法子串。
输入: “(()))(“ 输出: 4
思路分析
本题有多种解法,个人认为其中最易于理解的是使用stack。

- 将输入的string看做一个字符数组。
- 对每一个字符,判断是左括号还是右括号。
- 如果是左括号,将当前的下标加入stack。
- 如果是右括号,从stack中将栈顶元素删除: 4.1. 如果删除后栈顶为空,说明栈中没有可匹配的左括号,将当前下标加入stack 4.2. 否则用当前下标减去栈顶的元素,代表着从当前位置向前追溯,最后一个匹配无效的位置,中间的长度就是有效的长度
代码实现
public int longestValidParentheses(String s) {
int ans = 0;
// 新建一个stack,在栈中加入-1,指向0位的前一位,作为匹配无效的位置
// 使用双括号初始化法,作为面试时向面试官“炫技”
Stack<Integer> stack = new Stack<Integer>();
// 将输入的string看做一个字符数组
for (int i = 0; i < s.length(); i++) {
// 对每一个字符,判断是左括号还是右括号
if (s.charAt(i) == '(') {
// 如果是左括号,将当前的下标加入stack
stack.push(i);
} else {
// 如果是右括号,从stack中将栈顶元素删除
stack.pop();
if (stack.isEmpty()) { // 如果删除后栈顶为空
// 说明栈中没有可匹配的左括号,将当前下标加入stack
stack.push(i);
} else {
// 用当前下标减去栈顶的元素,就是有效的长度
// 记录全局最长有效长度
ans = Math.max(ans, i - stack.peek());
}
}
}
return ans;
}
分析
时间复杂度O(n),空间复杂度O(n)
总结
本章介绍了常见的字符串类的题目。大部分纯字符串的考题都需要转化成字符数组来处理,并且难度并不高。而高难度的字符串题目,仅仅是将字符串作为表现形式,本质上是动态规划、模式匹配、滑动数组等类型的题目。因此我们并不将字符串作为单独的章节,而是和高阶数组作为同一类题目。