Day 28 Dynamic Programming 动态规划 2
在之前的章节里,我们已经初步学习了动态规划类问题。这是面试算法题中最难的一类问题。然而面试算法题的考察面较小,70%以上的动态规划问题可以被划分进两个大类:背包/子集和问题,子序列/模式匹配问题。本章我们就来看子序列/模式匹配问题。
核心算法——子序列问题
子序列/模式匹配问题是面试中常考的经典动态规划类问题。一般表现为给出一个数组或字符串,找出符合某个模式的子串/子序列。或者给出两个数组或字符串,要求二者按照某种规则匹配。这类问题的解题思路相对固定,前者一般使用一维数组,后者使用二维数组。每次需要将原问题分解成子问题,子问题的性质和原问题相同但是规模较小。我们可以通过解决单步子问题来递推到原问题。
1.案例: 最长公共子序列
给出两个字符串,找到最长公共子序列(LCS),返回最长公共子序列的长度。
输入: str1 = “ZXVVYZW”, str2 = “XKYKZPW” 输出: 4
思路分析
最长公共子序列问题是一类经典的动态规划问题。一般要求在两个序列中找到最长公共子序列(子序列不需要是连续的子串)。假设我们有两个序列X & Y,我们想要找到X & Y的最长公共子序列LCS(X, Y),需要动态规划的思想,将原问题分解成子问题。
对于两个序列X & Y,每一步我们只需要考虑他们的最后一位:(假设下标分别为n & m)Xn & Ym
- 如果Xn = Ym,说明X的最后一位与Y的最后一位相同,那么该元素一定是公共子序列的一部分,LCS(Xn, Ym) = LCS(Xn - 1, Ym - 1) + 1
- 如果Xn != Ym,说明X的最后一位与Y的最后一位不同,该元素不属于公共子序列。我们需要排除Xn或者Ym,LCS(Xn, Ym) = max ( LCS(Xn, Ym - 1), LCS(Xn - 1, Ym))
我们用二维的dp数组来记录状态,dp[i][j]代表X序列前i个与Y序列的前j个的LCS长度
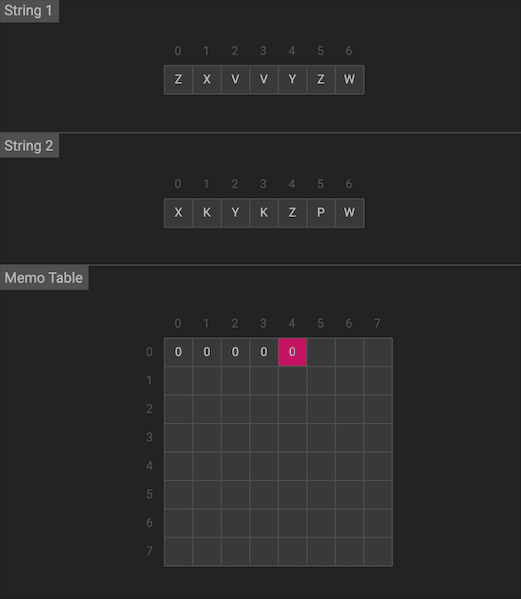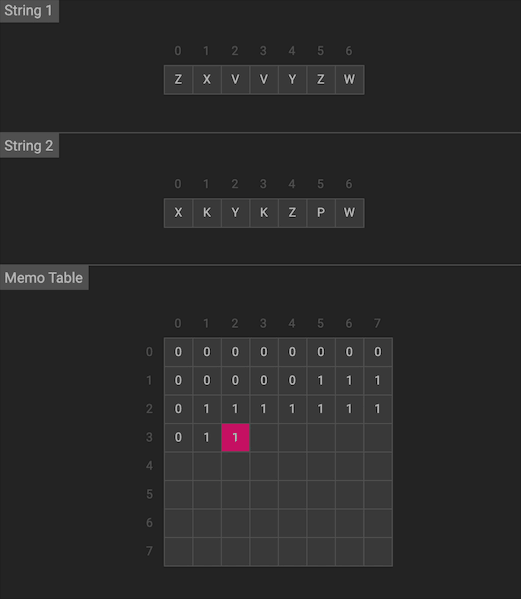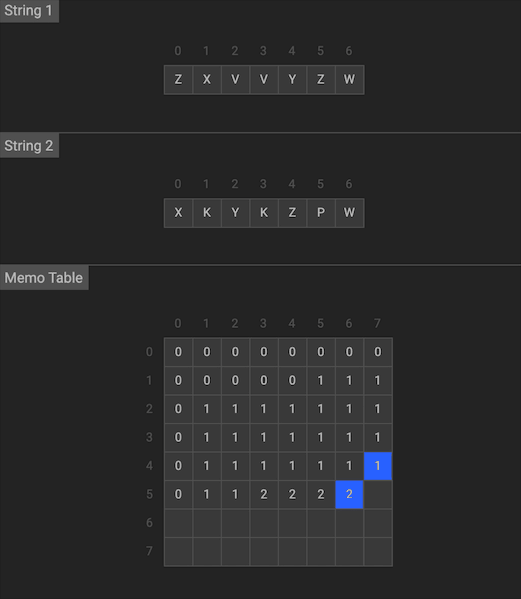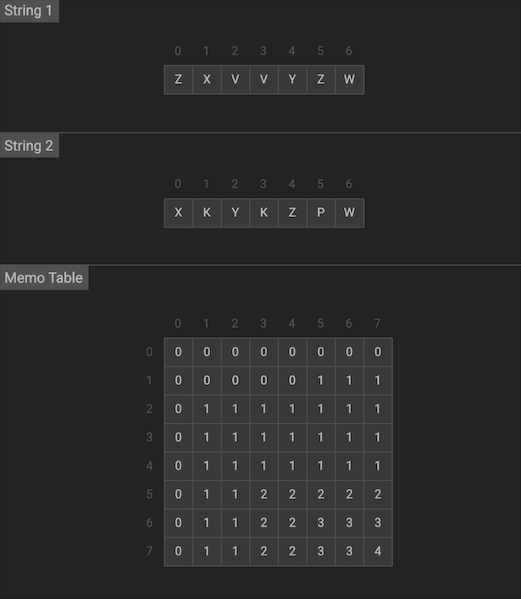
图片由visualgo制作
代码实现
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
// 初始化二维dp数组
int[][] dp = new int[m + 1][n + 1];
// 动态规划
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// X的最后一位与Y的最后一位相同
if (text1.charAt(i) == text2.charAt(j)) {
// LCS(Xn, Ym) = LCS(Xn - 1, Ym - 1) + 1
dp[i + 1][j + 1] = dp[i][j] + 1;
} else { // X的最后一位与Y的最后一位不同
// LCS(Xn, Ym) = max(LCS(Xn, Ym - 1), LCS(Xn - 1, Ym))
dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
}
}
}
// 返回LCS(X, Y)
return dp[m][n];
}
分析
时间复杂度O(nm),空间复杂度O(nm),n表示序列1的长度,m表示序列2的长度
2.案例: 最长的回文序列
给定字符串s, 找出在s中的最长回文子序列的长度.
输入: bbbab 输出: 4
思路分析
本题是LCS最长公共子序列问题的变种题。一个比较取巧的解法是将给出的字符串s,进行反转,分别得到正向和反向的字符串s和s’。然后利用上一题的方法求s和s’的LCS长度,即为s中的最长回文子序列的长度。
public int longestPalindromeSubseq(String s) {
return longestCommonSubsequence(s, (new StringBuilder(s)).reverse().toString());
}
这种方法比较取巧,我们另外介绍一种解法,依然利用动态规划的思想,将原问题分解成子问题。
我们用二维的dp数组来记录状态,dp[i][j]代表s[i…j]中最长回文序列的长度。初始化dp,长度为0时,dp[i][i] = 1。对于dp[i][j],
- 如果s[i] = s[j],说明s[i…j]的首尾对应,该元素属于回文序列的一部分,因此dp[i][j] = dp[i + 1][j - 1] + 2
- 如果s[i] != s[j],说明该元素不属于回文序列,我们需要排除s[i]或者s[j],dp[i][j] = max (dp[i + 1][j], dp[i][j - 1])
最后从dp[0][s.length - 1]得到结果
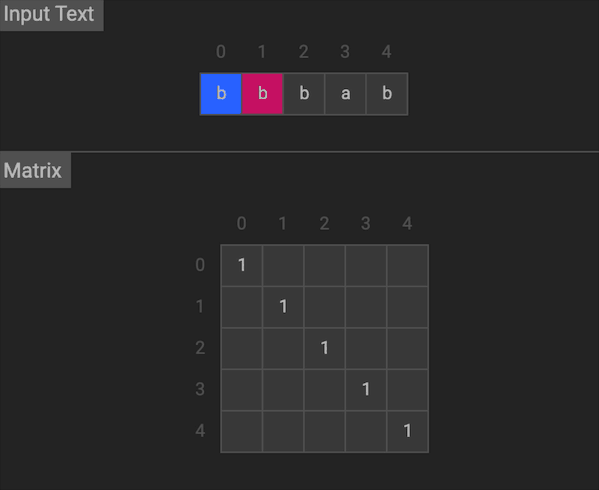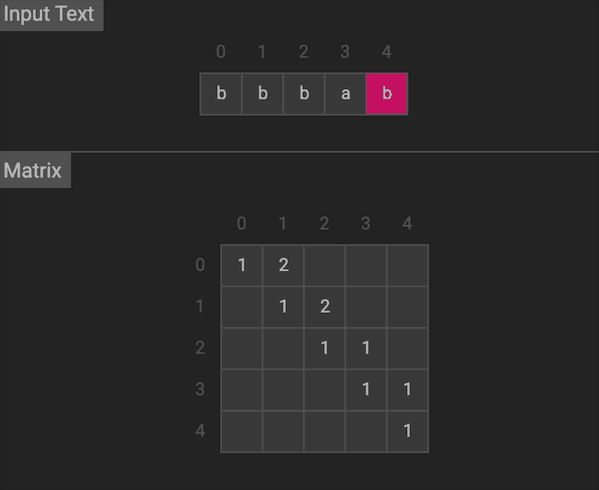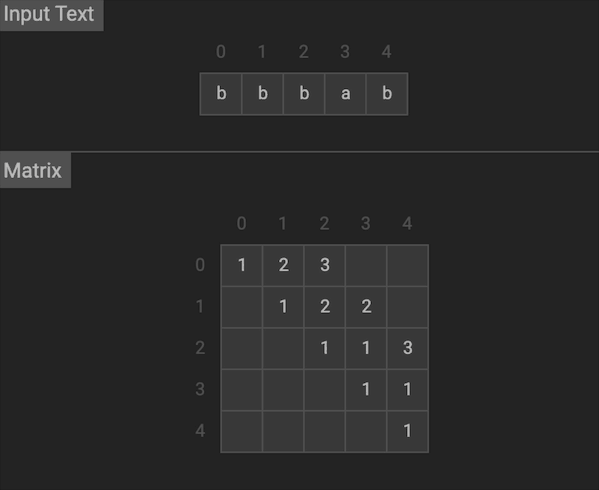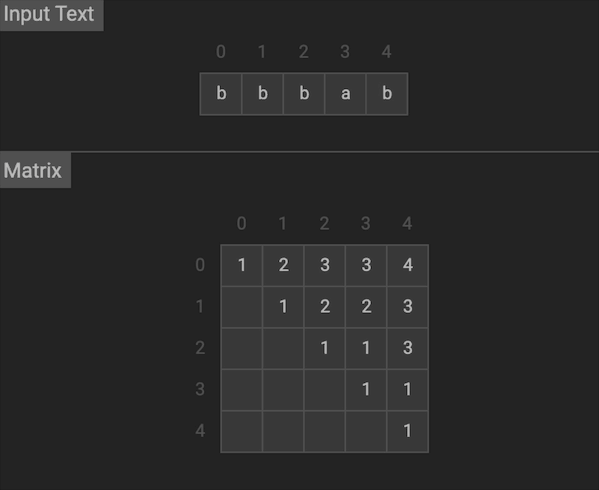
图片由visualgo制作
代码实现
public int longestPalindromeSubseq(String s) {
int length = s.length();
int[][] dp = new int[length][length];
// 初始化dp,dp[i][i] = 1
for (int i = 0; i < length; i++)
dp[i][i] = 1;
// 动态规划
for (int i = length - 1; i >= 0; i--) {
for (int j = i + 1; j < length; j++) {
// s[i] = s[j],该元素属于回文序列的一部分
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else { // s[i] != s[j]
// 排除s[i]或者s[j]
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
// 最终结果
return dp[0][length - 1];
}
分析
时间复杂度O(n2),空间复杂度O(n2)
3.案例: 莱文斯坦编辑距离
给定两个单词word1和word2,计算出将word1转换为word2的最少操作次数。总共有三种操作方法:插入/删除/替换
输入: str1 = “abc”, str2 = “yabd” 输出: 2
思路分析
本题是最常考的动态规划题之一,也是一道经典的二维dp题。取巧的解法依然是利用LCS最长公共子序列,先计算出两个单词的最长公共子序列。将s1转换成s2的过程中,LCS最长公共子序列是可以在转换前后保持不变的部分。换而言之,余下的字符都是需要编辑的,计算余下的字符个数,即为Levenshtein编辑距离。这里需要的是最长公共子序列,案例1仅仅计算了最长公共子序列的长度,所以需要对解法进行修改。这种方法实际上比较麻烦。因此我们另外介绍一种动态规划的解法,依然将原问题分解成子问题。
使用二维的dp数组来记录状态,dp[i][j]为word1前i个字符到word2的前j个字符的转化的最小编辑距离。对于每一步,
- 如果word1[i] = word2[j],说明word1[i]到word2[j]不需要转移,只要word1的前i-1个能转换到word2的前j-1个即可,所以dp[i][j] = dp[i-1][j-1]
- 如果word1[i] != word2[j],说明word1[i]到word2[j]需要转移,这时候有三种可能的操作:插入/删除/替换: 2.1. 给word1插入一个和word2最后的字母相同的字母,即 dp[i][j - 1] + 1 2.2. 删除word1的最后一个字母,即 dp[i - 1][j] + 1 2.3. 把word1的最后一个字母替换成word2的最后一个字母,即 dp[i - 1][j - 1] + 1
我们要选择三种中的最优情况 dp[i][j] = 1 + min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1])

图片由visualgo制作
代码实现
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
// 初始化dp,空字符串转化到长度为i的字符串距离为i
for (int i = 0; i <= m; i++)
dp[i][0] = i;
for (int i = 0; i <= n; i++)
dp[0][i] = i;
// 动态规划
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// word1[i]到word2[j]不需要转移
if (word1.charAt(i) == word2.charAt(j)) {
// word1的前i-1个转换到word2的前j-1个
dp[i + 1][j + 1] = dp[i][j];
} else { // word1[i]到word2[j]需要转移
// 选择插入/删除/替换,三种中的最优情况
dp[i + 1][j + 1] = 1 + Math.min(dp[i][j], Math.min(dp[i + 1][j], dp[i][j + 1]));
}
}
}
// 最终结果
return dp[m][n];
}
分析
时间复杂度O(nm),空间复杂度O(nm),n表示word1的长度,m表示word2的长度
4.案例: 最长上升子序列
给定一个整数序列,找到最长上升子序列(LIS),返回LIS的长度
输入: [4,2,4,5,3,7] 输出: 4 // [2,4,5,7]
思路分析
要寻找所有子序列中最长的那个,可以将原问题分解到每一步的子问题。在每一步,我们只需要找到当前最长的子序列。最后就能获得全局最长的子序列。
使用一个一维dp数组记录状态,dp[i]代表nums[0…i]之间以nums[i]结尾的最长子序列。初始时,每个位置以自己作为序列 dp[i] = 1。我们在每个位置上,遍历nums[0…i-1]找到能转移到nums[i]的序列,在最大长度上加1。可以得到递推公式 dp[i] = max {dp[j], 0 <= j <= i - 1} + 1
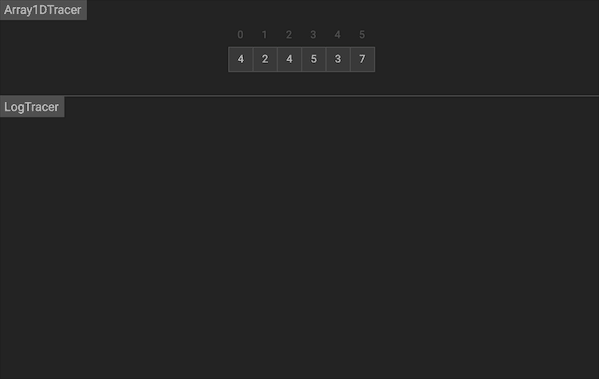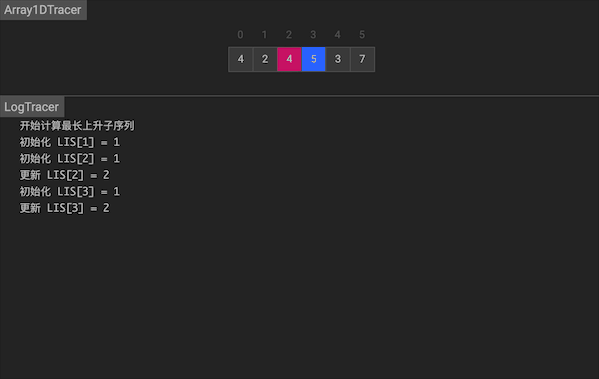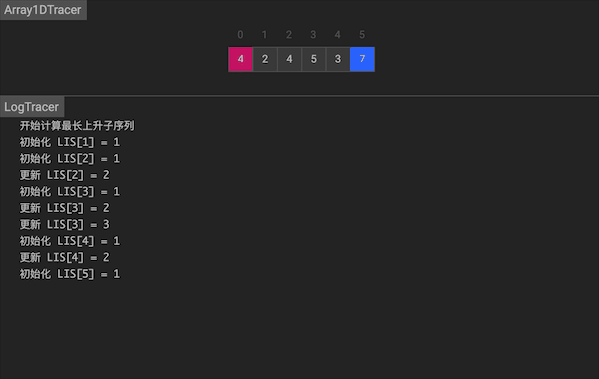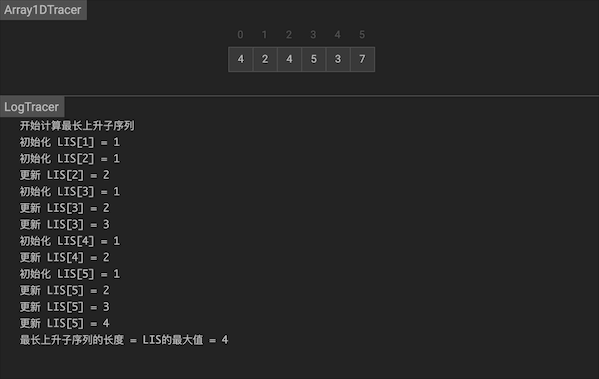
图片由visualgo制作
代码实现
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
int ans = 0;
// 动态规划
for (int i = 0; i < nums.length; i++) {
// 每个位置以自己作为序列
dp[i] = 1;
// 遍历nums[0...i-1]
for (int j = 0; j < i; j++) {
// 找到能转移到nums[i]的序列
if (nums[j] < nums[i])
// 最大长度上加1
dp[i] = Math.max(dp[i], dp[j] + 1);
}
// 全局最长子序列
ans = Math.max(dp[i], ans);
}
return ans;
}
分析
时间复杂度O(n2),空间复杂度O(n)
总结
本章我们学习了子序列问题,这类问题的出题模式固定一般会给定1-2个数组或字符串,解法固定可以使用1维或2维dp数组。这类题目一旦掌握了套路就可以快速解决,思路固定,代码实现相对简单。